There may be some trick that gives an easier way than to solve for all the
letters, but here it is that way:
 Solve the first two equations for a, by Cramer's rule:
Solve the first two equations for a, by Cramer's rule:

 Solve the 2nd and 3rd equations for a, by Cramer's rule:
Solve the 2nd and 3rd equations for a, by Cramer's rule:

 Set the first and second values for a equal:
Set the first and second values for a equal:
 Multiply both sides by
Multiply both sides by


 equation 1:
equation 1:  -----------------------------
Solve the 3rd and 4th equations for a, by Cramer's rule:
-----------------------------
Solve the 3rd and 4th equations for a, by Cramer's rule:

 Set the second and third values for a equal:
Set the second and third values for a equal:
 Multiply both sides by
Multiply both sides by
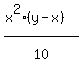

 equation 2:
equation 2:  Set the values of x from equations 1 and 2 equal
Set the values of x from equations 1 and 2 equal








 x and y cannot be equal because the first two given equations
would be inconsistent. For if they were equal, we'd have
x and y cannot be equal because the first two given equations
would be inconsistent. For if they were equal, we'd have
 Nultiplying thru by x gives
Nultiplying thru by x gives
 or that would give x=10, not what we got for y.
Therefore by symmetry of x and y, one of them has the + sign and the
other has the minus sign. So we choose them so that
or that would give x=10, not what we got for y.
Therefore by symmetry of x and y, one of them has the + sign and the
other has the minus sign. So we choose them so that
 and
and
 Since
Since

 , so
, so


 , so
, so

 Rationalizing the denominator we get
Rationalizing the denominator we get
 By symmetry, or by substituting,
By symmetry, or by substituting,
 So
So
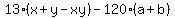



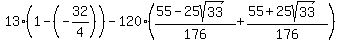
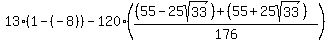
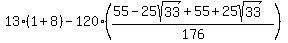
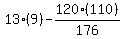
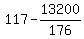
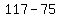
 Edwin
Edwin