Question 115143: I need to find the center,vertices, and foci of the ellipse
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website! I need to find the center,vertices, and foci of the ellipse
You first have to put it in standard form, which is either
(x - h)² (y - k)²
---------- + ---------- = 1
a² b²
if it turns out that the larger number is under
the term on the left which contains x, and the
graph will be an ellipse with a horizontal major
axis and a vertical minor axis, where
1. The center is (h, k)
2. The length of the semi-major axis is " a ".
3. The ends of the major axis are the points (h-a,k) and (h+a,k)
4. The ends of the minor axis are the points (h,k-b) and (h,k+b)
5. Foci are (h-c,k), (h+c,k) where c is calculated from c² = a²-b²
or
(x - h)² (y - k)²
---------- + ---------- = 1
b² a²
if it turns out that the larger number is under
the term on the left which contains y, and the
graph will be an ellipse with a horizontal major
axis and a vertical minor axis, where and the
graph will be an ellipse with a vertical major
axis and a horizontal minor axis
where
1. The center is (h, k)
2. The length of the semi-major axis is " a ".
3. The ends of the major axis are the points (h,k-a) and (h,k+a)
4. The ends of the minor axis are the points (h-b,k) and (h+b,k)
5. Foci are (h,k-a), (h,k+a) where c is calculated from c² = a²-b²
We can't tell which it is unti we get it into standard form:
4x² + 25y² - 8x + 100y + 4 = 0
Rearrange getting x² term then the x term then y²and y terms
That is, swap the second and third terms:
4x² - 8x + 25y² + 100y + 4 = 0
Subtract 4 from both sides:
4x² - 8x + 25y² + 100y = -4
Factor just the 4 out of the first two terms
on the left and also factor just the 25 out of
the last two terms on the left:
4(x² - 2x) + 25(y² + 4y) = -4
Complete the square in the first parentheses:
The coefficient of x is -2
Multiply it by  , getting -1
Square -1, getting +1.
Add +1 inside the first parentheses.
But the parentheses has a 4 in front.
So this amounts to adding 4·1 or 4 to
the left side, so we must add +4 to
the right side:
4(x² - 2x + 1) + 25(y² + 4y) = -4 + 4
Complete the square in the second parentheses:
The coefficient of y is 4
Multiply it by , getting 2
Square -2, getting +4.
Add +4 inside the first parentheses.
But the parentheses has a 25 in front.
So this amounts to adding 25·4 or 100 to
the left side, so we must add +100 to
the right side:
4(x² - 2x + 1) + 25(y² + 4y + 4) = -4 + 4 + 100
Factor both parentheses on the left and combine the
numbers on the right
4(x - 1)(x - 1) + 25(y + 2)(y + 2) = 100
4(x - 1)² + 25(y + 2)² = 100
To get a 1 on the right side, divide every term
by 100
4(x - 1)² 25(y + 2)² 100
--------- + ---------- = -----
100 100 100
Cancel
1 1 1
4(x - 1)² 25(y + 2)² 100
--------- + ---------- = -----
100 100 100
25 4 1
(x - 1)² (y + 2)²
---------- + ---------- = 1
25 4
Since 25 is greater than 4, and since a² is always the
larger or these in an ellipse, then a² is under the
term which contains x, we compare that to:
(x - h)² (y - k)²
---------- + ---------- = 1
a² b²
so it is an ellipse with a horizontal major axis and
a vertical minor axis. Comparing letters in this with
the numbers in the equation we got, we see that:
h = 1, k = -2, a² = 25, b² = 4 so a = 5 and b = 2
This means
1. The center is (h, k) = (1, -2)
2. The length of the semi-major axis is a = 5
3. The ends of the major axis (vertices) are the points (h-a,k), (h+a,k)
or (1-5,-2) and (1+5,-2) or (-4,-2) and (6,-2)
4. The ends of the minor axis are the points (h,k-b), (h,k+b)
or (1,-2-2), (1,-2+2) or (1,-4) and (1,0)
5. Foci are (h-c,k), (h+c,k) where c is gotten from c² = a²-b²
We calculate c:
c² = a² - b²
c² = 5² - 2²
c² = 25 - 4
c² = 21
c = Ö21 __ __
So foci are (h-c,k) and (h+c,k), or (1-Ö21,-2) and (1+Ö21),
or about (-3.6,-2) and (5.6,-2)
We draw the major and minor axes and plot the foci:
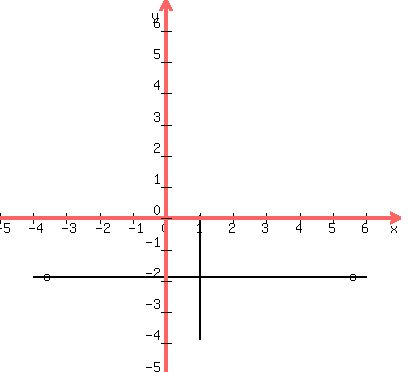Then we sketch in the ellipse:
The answers to your problem are:
center = (1, -2)
vertices = ends of major axis = (-4,-2) and (6,-2)
foci = (1-Ö21,-2) and (1+Ö21,-2),
Edwin
|
|
|
