SOLUTION: 1) suppose (x^2)+(y^2)=1 is a known identity. Determine if, under such assumption, the following is an identity: 2(y^6)+(x^5)=-2(x^6)+(x^5)+6(x^4)-6(x^2)+2 A) NOT an identity B)

We want to show that if x and y are REAL numbers that satisfy the 2nd equation,
they also satisfy the 1st equation.  That is to say that there are no REAL
numbers which satisfy the second equation which do not satisfy the first
equation. 

Suppose x and y are REAL numbers that satisfy this equation:



Subtract x^5 from both sides



Divide through by -2



Recognize the right side as the expansion of (x²-1)³



Take cube roots of both sides:



Subtract x² from both sides



Multiply through by -1



Yes it is an identity because x and y also satisfy x² + y² = 1 

-------------------------------

We want to prove or disprove that any REAL value of x which satisfies



and therefore this
  <-- second equation

also satisfies 

 
and therefore
  <-- first equation 

Let x be a REAL number that satisfies
 


We wonder if the first polynomial on the left of the first equation is a factor
of the polynomial on the left of the second one, so we divide by long division
to see:

                    x^3+ x^2- x-3
x^2- x+ 2)x^5+0x^4+0x^3+0x^2+ x-6
          x^5- x^4+2x^3
               x^4-2x^3+0x^2
               x^4- x^3+2x^2
                   -x^3-2x^2+ x
                   -x^3+ x^2-2x
                       -3x^2+3x-6
                       -3x^2+3x-6
                                0 


The remainder is zero, so indeed it is a factor. Therefore

 is equivalent to


Every odd degree polynomial has at least one REAL solution.
Let r be a REAL solution of .
Then r is a REAL solution of .
However r cannot satisfy  for its discriminant
is negative and it has no REAL solutions.

So  is not an identity, under the assumption
that  is an identity.

Edwin

Edwin made a huge and a perfect job solving these problems and explaining it to you.


But I still want to return to the problem.


    - Why ?


Because I think that its formulation is FAR FROM TO BE precisely perfect and correct.


So, I want to concentrate my and your attention on matters that were, probably, out the scope of the visitor, 
of the author of the problem and even out the Edwin's scope.


What Edwin proved, is THIS:


    If   = 1,     (1)  

        then  

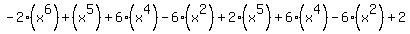      = .      (2)


Mathematicians express it by these words:

    if  values of x and y satisfy equation (1), then they satisfy also equation (2).



Or by these words: 

    if the set of points {(x,y)} satisfy equation (1), then this set of points satisfy equation (2), also.



Or by these words:

    equation (2) is satisfied on the set of solutions of equation (1).



Notice that I do not use the words 

    "the following is an identity   = -2(x^6) + (x^5) + 6(x^4) - 6(x^2) + 2(x^5) + 6(x^4) - 6(x^2) + 2}}}"    (*)


because the literal meaning of these words is that the identity (*) is true for ALL VALUES of variables x and y.


The last statement, OBVIOUSLY, would be FALSE and WRONG.



So, actually, the correct formulation to problem (1) would be 


    Prove that the first given equation is equivalent to the second given equation on the coordinate plane.

Same or very similar note about the problem (2).


Its correct formulation would be


    Check if the first given equation is equivalent to the second given equation.


Edwin showed that the first given polynomial is a factor to the second given polynomial.

Therefore, every solution to the first polynomial is the solution to the second polynomial.


But the second polynomial has other factor and, via this factor, has other solution, which is not the solution to the first equation.


So, the first and the second given equations ARE NOT EQUIVALENT.