Question 1151395: If the random variable X has uniform distribution on the interval [0,a] then
what is the probability that the random variable greater than its square i.e.
P(x > x^2)?
Found 2 solutions by Edwin McCravy, ikleyn:
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
Answer by ikleyn(52884)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
1) First, let's consider the case a < 1.
Then for all values of x in the segment [0,a] x > x^2 (which is ABSOLUTELY OBVIOUS).
So, if a < 1, then P(x > x^2) = 1.
2) Next, consider the case a >= 1.
Then x > x^2 if and only if 0 <= x < 1.
Therefore, P(x > x^2) = 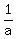 ( since the random variable x has uniform distribution on the interval [0,a]).
3) Thus the final ANSWER / (the final formula) is THIS :
if the the random variable X has uniform distribution on the interval [0,a] then
the probability that the random variable is greater than its square, i.e. P(x > x^2), is equal to 1, if a < 1
and
the probability that the random variable is greater than its square, i.e. P(x > x^2), is equal to ( since the random variable x has uniform distribution on the interval [0,a]).
3) Thus the final ANSWER / (the final formula) is THIS :
if the the random variable X has uniform distribution on the interval [0,a] then
the probability that the random variable is greater than its square, i.e. P(x > x^2), is equal to 1, if a < 1
and
the probability that the random variable is greater than its square, i.e. P(x > x^2), is equal to 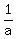 , if a >= 1. , if a >= 1.
Solved.
/\/\/\/\/\/\/\/
Notice, I edited my post after receiving a note from Edwin.
What you see now in my post is the final version.
Thanks to Edwin for his note.
|
|
|