Question 1151389: A diagnostic test for a certain disease is said to be 90% accurate in that, if a person has the disease, then the test will detect with probability 0.9.
Also, if a person does not have the disease, then the test will report that he or she doesn’t have it with probability 0.9. Only 1% of the population has the disease in question. If the diagnostic test reports that a person chosen at random from the population has the disease, then what is the conditional probability that the person, in fact, has the disease?
Answer by VFBundy(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! We are given this info:
Chances a person with the disease tests positive = 0.90 [GIVEN]
Chances a person with the disease tests negative = 0.10
Chances a person without the disease tests positive = 0.10
Chances a person without the disease tests negative = 0.90 [GIVEN]
It is also given that the person chosen at random tests positive for the disease, so we are only concerned with:
Chances a person with the disease tests positive = 0.90
Chances a person without the disease tests positive = 0.10
We also know that only 1% of the population actually has the disease, so the above needs to be weighted as such:
Chances a person with the disease tests positive = 0.90 * 0.01 = 0.009
Chances a person without the disease tests positive = 0.10 * 0.99 = 0.099
We want to find the probability that the random person who tested positive actually has the disease, so we compute that as such:
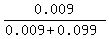 = = 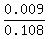 = 0.0833 = 0.0833
|
|
|