Question 1151386: Belle, who has just started her first full-time salary job is determined to have $1 million in her account by the time she retires. She is now 25 and hopes to retire at 65 years of age. Her investments have been earning 6.25% annual return and she thinks it’s realistic that can be maintained.
i
How much would Belle have to put aside each month, in order to reach her goal? [I solved and the answer is 469.06)
What is the total amount of money she will have saved? [2]
How much interest will have been earned? [3]
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
As the problem is worded, printed, posted and presented, it is not complete and, therefore, is not fully accurate.
To be accurate, it should say that
a) the account is compound;
b) it should say what is the compound period, and
c) does she pay at the beginning or at the end of the compound period.
So, I will assume that the account is compound; the compound period is 1 month, and she pays at the end of each month.
Then it is a classic Ordinary Annuity saving plan. The general formula is
FV =  ,
where FV is the future value of the account; P is the monthly payment (deposit); r is the monthly percentage yield
presented as a decimal; n is the number of deposits (= the number of years, 40, multiplied by 12, in this case).
From this formula, you get for the monthly payment
P = ,
where FV is the future value of the account; P is the monthly payment (deposit); r is the monthly percentage yield
presented as a decimal; n is the number of deposits (= the number of years, 40, multiplied by 12, in this case).
From this formula, you get for the monthly payment
P =  . (1)
Under the given conditions, FV = $1,000,000; r = 0.0625/12; n = 40*12. So, according to the formula (1), you get
for the monthly payment
P = . (1)
Under the given conditions, FV = $1,000,000; r = 0.0625/12; n = 40*12. So, according to the formula (1), you get
for the monthly payment
P = 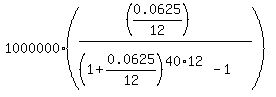 = $469.07.
Answer. The necessary monthly deposit value is $469.07.
Note that of projected $1,000,000 the total of her deposits will be only 40*12 times $469.07,
i.e. 40*12*469.07 = 225,153.60 dollars. The rest is what the account will earn/accumulate in 40 years. = $469.07.
Answer. The necessary monthly deposit value is $469.07.
Note that of projected $1,000,000 the total of her deposits will be only 40*12 times $469.07,
i.e. 40*12*469.07 = 225,153.60 dollars. The rest is what the account will earn/accumulate in 40 years.
---------
On Ordinary Annuity saving plans, see the lessons
- Ordinary Annuity saving plans and geometric progressions
- Solved problems on Ordinary Annuity saving plans
in this site.
The lessons contain EVERYTHING you need to know about this subject, in clear and compact form.
When you learn from these lessons, you will be able to do similar calculations in semi-automatic mode.
|
|
|