Question 1151382: The function  has a relative maximum at the point (-2,27) and a relative minimum at the point (1,0). Find the values of a, b, c and d. has a relative maximum at the point (-2,27) and a relative minimum at the point (1,0). Find the values of a, b, c and d.
I end up with 4 equations the I need to solve simultaneously. Is there a better method?
Answer by ikleyn(52915)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
First derivative is
y' = 3ax^2 + 2bx + c.
According to the condition, it has zeroes at x= -2 and x= 1.
Hence, 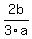 = - = - 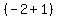 = 1 and = 1 and 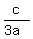 = -2
(according to Vieta's theorem).
From these equalities,
b = = -2
(according to Vieta's theorem).
From these equalities,
b = 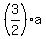 and c = -6a. (*)
Substitute these values to the equation for y. You will get
y = and c = -6a. (*)
Substitute these values to the equation for y. You will get
y =  + + 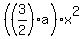 - - 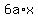 + d. (1)
Substitute x = -2 into (1) to get y = 27. It gives you
27 = -8a + 6a + 12a + d, or
27 = 10a + d. (2)
Substitute x = 1 into (1) to get y = 0. It gives you
0 = a + + d. (1)
Substitute x = -2 into (1) to get y = 27. It gives you
27 = -8a + 6a + 12a + d, or
27 = 10a + d. (2)
Substitute x = 1 into (1) to get y = 0. It gives you
0 = a + 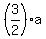 - 6a + d, or
0 = 2a + 3a - 12a + 2d, or
0 = -7a + 2d. (3)
Thus you have the system of 2 equations in 2 unknowns
10a + d = 27, (2')
-7a + 2d = 0. (3')
From (2'), express d = 27-10a and substitute it into (3'). You will get
-7a + 2*(27-10a) = 0,
-7a + 54 - 20a = 0
54 = 7a + 20a
54 = 27a
a = 54/27 = 2.
Thus a = 2, d = 27 - 10a = 27 - 20 = 7.
Finally, from (*)
b = - 6a + d, or
0 = 2a + 3a - 12a + 2d, or
0 = -7a + 2d. (3)
Thus you have the system of 2 equations in 2 unknowns
10a + d = 27, (2')
-7a + 2d = 0. (3')
From (2'), express d = 27-10a and substitute it into (3'). You will get
-7a + 2*(27-10a) = 0,
-7a + 54 - 20a = 0
54 = 7a + 20a
54 = 27a
a = 54/27 = 2.
Thus a = 2, d = 27 - 10a = 27 - 20 = 7.
Finally, from (*)
b = 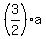 = =  = 3, and
c = -6a = -6*2 = -12.
ANSWER. a = 2; b = 3; c = -12; d = 7. = 3, and
c = -6a = -6*2 = -12.
ANSWER. a = 2; b = 3; c = -12; d = 7.
Solved.
|
|
|