SOLUTION: Tickets numbered 2 to 101 are placed in a box and a single ticket is chosen at random. Find the probability of selecting a ticket with a number contains the digit 5

This problem is easy to solve.


First, you need to find the number of tickets, containing the digit of 5.

Second, you need to relate this number to the total number of tickets.



Let start finding the number of tickets, containing the digit of 5.



These tickets may have the digit of 5 as their last digit (the "ones" digit):

    5, 15, 25, . . . , 85, 95,

and the number of this kind of tickets is 10, OBVIOUSLY.



These tickets also may have the digit of 5 as the first digit (the "tens" digit):

    50, 51, 52, . . . , 59,

and the number of this kind of tickets is 10, again.



Therefore, the full number of tickets having the digit of 5 is  10+10-1 = 19.

I must subtract the "1" from the sum of 10+10, because I count the ticket  "55"  twice: in the first and in the second category.



The total number of tickets is  101-1 = 100, OBVIOUSLY.



Thus the probability under the question is  P = 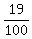 = 0.19 = 19%.    ANSWER