Question 1151348: Construct a difference table to predict the next term of the sequence
-1,4,21,53,103,174,269,...
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A table showing the original sequence and the rows of first, second, and third differences:
-1 4 21 53 103 174 269
5 17 32 50 71 95
12 15 18 21 24
3 3 3 3
There is a constant difference of 3 in the row of third differences. To find the next term in the sequence, place another difference of 3 in the third row and work back up the array:
-1 4 21 53 103 174 269 391
5 17 32 50 71 95 122
12 15 18 21 24 27
3 3 3 3 3
The predicted next term of the sequence is 391.
By the way.... The constant difference in the row of third differences means the sequence is generated by a polynomial of degree 3. The coefficient of the leading term is the constant difference (3) divided by the factorial of the degree of the polynomial (3!=6). So the coefficient of the leading term is
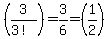
and the leading term of the polynomial is then
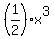
|
|
|