SOLUTION: in an A.P the 8th term is twice the 4th term and the 20th term is 40 .find the common difference and the sum of terms from the 8th to the 20th.

From the first part of the condition,


    a + 7d = 2*(a + 3d),


where "a" is the 1-st term of the AP and "d" is the common difference.


From this equation


    a + 7d = 2a + 6d,

    7d - 6d = 2a - a

     d      = a.      (1)


We are given also


     a + 19d = 40,


which implies, due to (1)


     20d = 40,

       d = a = 2.


Thus, in this AP the first term is 2 and the common difference is 2, too.


So, the 8-th term is  2+2*7 = 16  and  the 20-th term is  40  (given (!) ).


The average of the 8-th term and the 20-th term is, therefore, 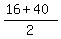  = 28.


The sum of the terms from the 8-th term to 20-th term (inclusive) is the product of this mean value 28 
by the number of terms, which is (20-7) = 13.


Thus the sum is 28*13 = 364.    ANSWER