SOLUTION: What is the sum of all integral values of x for which 18(x^2-7x+10)/(x^3-6x^2+3x+10) is a positive integer?

Algebra ->  Expressions-with-variables -> SOLUTION: What is the sum of all integral values of x for which 18(x^2-7x+10)/(x^3-6x^2+3x+10) is a positive integer?      Log On


   

Question 1151162: What is the sum of all integral values of x for which
18(x^2-7x+10)/(x^3-6x^2+3x+10) is a positive integer?
Found 2 solutions by ikleyn, Edwin McCravy:
Answer by ikleyn(52813) About Me  (Show Source):
You can put this solution on YOUR website!
.
What is the sum of all integral values of x for which 18(x^2-7x+10)/x^3-6x^2+3x+10?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~


As your post is worded, printed, submitted and presented,  IT  MAKES  NO  SENSE.



Answer by Edwin McCravy(20060) About Me  (Show Source):
You can put this solution on YOUR website!
She's right.  I just guessed and added the words "is a positive integer" so your
sentence would make sense. I also put parentheses around (x^3-6x^2+3x+10) so
that the whole thing would be the denominator and not just the first term x^3 by
the PEMDAS rule.

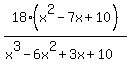18%28x%5E2-7x%2B10%29%2F%28x%5E3-6x%5E2%2B3x%2B10%29

Factoring, using synthetic division to factor the denominator,

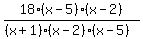18%28x-5%29%28x-2%29%2F%28%28x%2B1%29%28x-2%29%28x-5%29%29

Canceling the (x-5)'s and the (x-2)'s

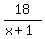18%2F%28x%2B1%29 must be a positive integer.

x+1 must be a factor of 18.  The factors of 18 are 1,2,3,6,9,18.

x+1 = 1,2,3,6,9,18
  x = 0,1,2,5,8,17

Adding: 0+1+2+5+8+17 = 33 

That's the answer if I happen to have guessed the right words to add to make
what you wrote make sense.

Edwin