Question 1151124: Three positive numbers form an arithmetic progression; their sum is 18. If the first number is increased by 4, then the numbers will form a geometric progression. Find the original three numbers in arithmetic progression.
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Three positive numbers form an arithmetic progression; their sum is 18. If the first number is increased by 4,
then the numbers will form a geometric progression. Find the original three numbers in arithmetic progression.
~~~~~~~~~~~~~~~~~~~~~~~~~~
Since the three numbers form an AP with the sum 18, the middle terms is 18/3 = 6.
Let "d" be the common difference of this AP.
Then the three terms of the AP are 6-d, 6 and 6+d.
Then the three terms of the GP are ((6-d)+4) = 10-d, 6 and 6+d.
Since the terms 10-d, 6 and 6+d form a GP,
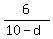 = = 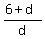 .
It is your equation to find "d". Cross multiply
6d = (10-d)*(6+d)
6d = 60 - 6d + 10d - d^2
d^2 + 2d - 60 = 0 .
It is your equation to find "d". Cross multiply
6d = (10-d)*(6+d)
6d = 60 - 6d + 10d - d^2
d^2 + 2d - 60 = 0
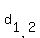 = =  = = 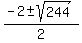 = = 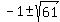 .
With the middle term 6, NEITHER value of d = .
With the middle term 6, NEITHER value of d = 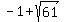 = 6.81... NOR d = = 6.81... NOR d = 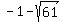 = -8.81...
provides three positive terms of the AP.
ANSWER. As the problem is worded, printed, posted and presented, the solution DOES NOT exist. = -8.81...
provides three positive terms of the AP.
ANSWER. As the problem is worded, printed, posted and presented, the solution DOES NOT exist.
F A K E problem.
|
|
|