Question 1151123: Suppose on a nice December evening you gaze upon your favorite star. You stick your handout into the sky and point at it, then you keep your arm fixed and frozen. Until 6 months later when you reach for the sky again and point at your star with your other arm. Suppose now you observe the angle you have created with your arms to be 0.14°. How far is the star from the sun? [hint: assume the earth orbits in a circular motion around the sun once every 12 month, where the orbit has radius of r=149.6×10^6 km]
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
With the given data, in general case, the distance to the star CAN NOT be determined.
In order for it COULD be determined, at least one additional input value should be given : the angle between the direction
of the diameter at that time and the averaged direction to the star.
What CAN BE estimated and calculated, is the maximum possible distance
d = 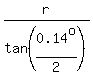 = = 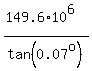 = approximately = = approximately =  = 1.23*10^11 kilometers, based on the given data.
Notice that the nearest star to the Earth, Proxima Centauri, is, actually, 40,208,000,000,000 km away from the Earth,
according to VERY RELIABLE sources (see, for example, https://imagine.gsfc.nasa.gov/features/cosmic/nearest_star_info.html ) = 1.23*10^11 kilometers, based on the given data.
Notice that the nearest star to the Earth, Proxima Centauri, is, actually, 40,208,000,000,000 km away from the Earth,
according to VERY RELIABLE sources (see, for example, https://imagine.gsfc.nasa.gov/features/cosmic/nearest_star_info.html )
So, the post gives TOTALLY WRONG input data and represents, thus, a F A K E P R O B L E M.
|
|
|