Question 1151086: A master dog trainer lined up 255 highly intelligent dogs in front of him, numbering them from 1 to 255, from left to right. He shouted “Sit!” and all the dogs sat down. Then he shouted, “Switch 2!” and all the dogs with an even number stood up. When the trainer shouted “Switch 3!” all the dogs with numbers divisible by three sat down if they were standing or stood up if they were sitting. He continued to shout, “Switch 4! Switch 5!” and so on until “Switch 255!” At the end of the exercise, how many dogs were sitting down?
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
At the end of the exercise, those and only those dogs will be sitting, whose numbers are perfect squares, like 1, 4, 9, 16, . . . .
The number of perfect squares from 1 to 255 is the integer part of the number 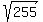 = 15.97, i.e. 15.
ANSWER. At the end of the exercise, 15 dogs will be sitting.
---------------
For the full solution to the similar problem, see the lesson
- Math Circle level problem on lockers and divisors of integer numbers
in this site.
|
|
|
