SOLUTION: A BOAT TRAVELS 52 MILES UP THE RIVER IN THE SAME AOUNT OF TIME IT TAKES TO TRAVEL 92 MILES DOWN THE SAME RIVER. IF THE CURRENT IS 5 MILES PER HOUR, WHAT IS THE SPEED OF THE BOAT IN

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: A BOAT TRAVELS 52 MILES UP THE RIVER IN THE SAME AOUNT OF TIME IT TAKES TO TRAVEL 92 MILES DOWN THE SAME RIVER. IF THE CURRENT IS 5 MILES PER HOUR, WHAT IS THE SPEED OF THE BOAT IN      Log On


   

Question 115098: A BOAT TRAVELS 52 MILES UP THE RIVER IN THE SAME AOUNT OF TIME IT TAKES TO TRAVEL 92 MILES DOWN THE SAME RIVER. IF THE CURRENT IS 5 MILES PER HOUR, WHAT IS THE SPEED OF THE BOAT IN STILL WATER ?
Answer by solver91311(24713) About Me  (Show Source):
You can put this solution on YOUR website!
HEY! Ease up on the ALL CAPS.

Remember the formula for distance, rate, and time: d=rt.

We want to find the boat's speed through the water, so lets call that r.

The boat goes up river against the current, so the speed relative to the land is 5 miles per hour less than the speed through the water, or r - 5.

The boat goes down river with the current, so the speed is 5 mph more, or r + 5.

First let's rearrange the formula so that it is in terms of time: t=d%2Fr

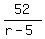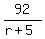The amount of time the boat traveled up river is then given by 52%2F%28r-5%29 and the time down river is given by 92%2F%28r%2B5%29. And we know from the problem statement that these two times are equal, so:

92%2F%28r%2B5%29=52%2F%28r-5%29

92%28r-5%29=52%28r%2B5%29, Cross-multiply the proportion

92r-460=52r%2B260, Distribute

92r-52r=260%2B460, Collect like terms
40r=720

r=18, Divide by 40

And the speed of the boat through the water is 18 miles per hour.

Last step, VERY important: Check your answer.
52%2F%2818-5%29=52%2F13=4
92%2F%2818%2B5%29=92%2F23=4 Since both times (4 hours) are equal, the answer checks.

Hope that helps,
John