|
Question 1150903: Vanessa, the student council president, needed to get a message to the whole school, so she set up an email tree. She sent the message to the two vice presidents and made them forward it to two other students. Suppose the pattern is repeated and no student receives it more than once!
a) How many people receive it during the seventh mailing?
b) Which mailing will be sent to 500 people?
c) There are 500 students in the school, so how many does it take to send the mail to all of them?
Found 2 solutions by MathLover1, jim_thompson5910:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are two components here, how many receive the new email in a round, and the total of students that have been informed.
Each time an email is sent, it reaches  as many people as the time before. So the pattern is as many people as the time before. So the pattern is  , , , , , ,  , ,  , ,  , ,  , ,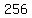 , ,  , etc. , etc.
This is  , where , where  is a particular is a particular 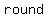 of mailing. of mailing.
Now when this starts, Vanessa knows, that's  person. After the first mailing, it's person. After the first mailing, it's 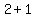 people that know, next it's people that know, next it's 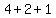 , then , then , etc. You might recognize this as , etc. You might recognize this as 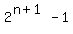 . .
a) How many people receive it during the 7th mailing?
use  , where , where  is a particular is a particular 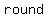 of mailing of mailing
so, in your case 
 people people
b) Which mailing will be sent to  people? people?
Since we already know that  , let's keep going from there. , let's keep going from there.



Since we have exceeded  , we stop there. , we stop there.
So, we know that since the power is  , the email has been sent , the email has been sent  times. times.
c) There are 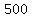 students in the school, so how many does it take to send the mail to all of them? students in the school, so how many does it take to send the mail to all of them?
This question was already answered in part b). The answer is 
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Part a)
During the nth mailing, 2^n students will be messaged. So for the first mailing (n=1) we have 2^n = 2^1 = 2 students messaged (the two vice presidents). Then for round two (n=2), we have 2^n = 2^2 = 4 students messaged in this round.
For the 7th mailing, plug n = 7 into 2^n to get 2^n = 2^7 = 128.
Answer: 128
====================================================
Part b)
Think backwards from part a). We want to aim for 500 students in a single round of messaging. The question is "what value of n will make 2^n equal 500?".
We want to solve
2^n = 500
Use logarithms to answer that question. You will need your calculator.
2^n = 500
Log(2^n) = Log(500)
n*Log(2) = Log(500)
n = Log(500)/Log(2)
n = 8.96578428466209
Note how if n = 8, then
2^n = 2^8 = 256
and when n = 9, we have
2^n = 2^9 = 512
so as expected, the solution is somewhere in between n = 8 and n = 9
Using n = 8 is too small, so we have to go with n = 9
Answer: 9th round
====================================================
Part c)
Here is a list of powers of 2
1,2,4,8,16,32,64,128,256,512,...
Let's compute partial sums
1+2 = 3
1+2+4 = 7
1+2+4+8 = 15
1+2+4+8+16 = 31
1+2+4+8+16+32 = 63
1+2+4+8+16+32+64 = 127
1+2+4+8+16+32+64+128 = 255
1+2+4+8+16+32+64+128+256 = 511
Each sum is 1 less than the next power of 2. The general formula is

What this means is that we can quickly compute how many students have been messaged in total (rather than just on an individual round).
Set 2^(n+1) - 1 equal to 500 and solve for n.
2^(n+1) - 1 = 500
2^(n+1) = 500+1
2^(n+1) = 501
Log(2^(n+1)) = Log(501)
(n+1)*Log(2) = Log(501)
n+1 = Log(501)/Log(2)
n+1 = 8.9686667931952
n = 8.9686667931952-1
n = 7.9686667931952
That rounds to n = 8
By round 8, a total of
2^(n+1)-1 = 2^(8+1)-1 = 511
people have been messaged
If we ignore Vanessa, then 511-1 = 510 people have been messaged
Of course this school has 500 students and not 510 or 511. The same value of n is the answer however because in the 8th round 2^8 = 256 people are messaged. Subtracting 11 from this count is still a positive value.
Answer: 8th round
As you can see, there is no need to have a 9th round in which 512 people are messaged because the entire school will be notified by the 8th round
1+2+4+8+16+32+64+128+256 = 511
note that 2^n = 2^8 = 256
|
|
|
| |