Question 1150893: Textbook authors and publishers work very hard to minimize the number of errors in a text. However, some errors are unavoidable. Mr. J. A. Carmen, statistics editor, reports that the mean number of errors per chapter is 0.8 . What is the probability that there are less than 2 errors in a particular chapter?
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let the event an 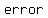 appearing in a chapter be a appearing in a chapter be a  . .
Let " " represent the number of " represent the number of  . .
The number of errors in a chapter can be either  , , , , ,... ,...
==> " " can carry the values " can carry the values  , , , , , , ,... ,...
==> " " is a discrete random variable with range = { " is a discrete random variable with range = {  , , , , },..... [Countably infinite] },..... [Countably infinite]
The probability distribution of " " is a " is a  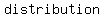 . .
Since there are a large number of trials all of which are identical and independent with only two possible outcomes in each trial, either a success (there being an error) or a failure (there not being an error), with the probability of success in all the trials remaining the same all thought.
The probability function of a Poisson distribution
==> 
Parameter of the distribution
==> Mean of the distribution
==> Mean number of errors per chapter =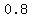
==> m = 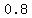
Therefore 
Probability that there are less than 2 errors in a chapter
==>
= 
= 
= 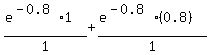
= 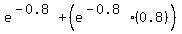
=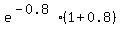
= 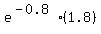
=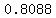 approximately approximately
|
|
|