Question 1150864: Good evening and Happy New Year to all Algebra Tutors!
What is the largest seven-digit number divisible by 44 that can be formed by the digits 1, 2, 3, 4, 6, 7, and 8 each used exactly once?
Found 5 solutions by Alan3354, MathLover1, math_helper, MathTherapy, jim_thompson5910:
Answer by Alan3354(69443)   (Show Source):
You can put this solution on YOUR website! What is the largest seven-digit number divisible by 44 that can be formed by the digits 1, 2, 3, 4, 6, 7, and 8 each used exactly once?
------------
Start with 8764321.
8764321/44 = 199189.1136
----
44*199189 = 8764316
==========
By subtracting 44 repeatedly ----> 8761324
--------
I don't think there's an algebraic method to solve this, and I don't think there's anything to learn from it.
=================
I first missed the fact that there is no 5.
MathLover added a 9.
----
Still, IMO, it's a useless problem.
Maybe New Year's Day is not a good day to do math?
----
Most importantly, no animals were injured in the process.
Answer by MathLover1(20849)  (Show Source):
You can put this solution on YOUR website! the largest 7 digit number formed by the digits 1, 2, 3, 4, 6, 7, and 8 each used exactly once is 
First we have to divide by  :  
We get 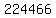 as the quotient and  as the remainder.
To get the answer, subtract the remainder from the dividend, i.e., from
We get,
So  is the largest  digit multiple of .
Answer by math_helper(2461)  (Show Source):
You can put this solution on YOUR website! 8761324
According to the problem statement, the seven digits are { 8,7,6,4,3,2,1 }, note that there is no 0, 5, 9.
I found the number as follows (I do NOT claim this to be the most efficient method):
8800000 clearly divisible by 44. Subtract 44 to get:
8799956 subtract 33000 (= 44*750) to get:
8766956
from here, realizing we need to use the digits 1,2,3,4 in the last 4 places,
I tried different combinations (ending with the 2 or 4) to arrive at:
8761324 (=199121*44)
Answer by MathTherapy(10549)  (Show Source):
You can put this solution on YOUR website! Good evening and Happy New Year to all Algebra Tutors!
What is the largest seven-digit number divisible by 44 that can be formed by the digits 1, 2, 3, 4, 6, 7, and 8 each used exactly once?
I don't know where ALAN got 8 digits. It's clear that there're 7.
MATHLOVER!, as usual, I don't know how to make sense of what she's TRYING to say. Why on earth did she OMIT 1 and 2, and ADD 0, 5, and 9 when trying
to determine the largest 7-digit number from the given digits? From the given digits, isn't the largest 7-digit number, 8,764,321? Makes NO SENSE at all to me!!
The correct answer's: 
Answer by jim_thompson5910(35256)  (Show Source):
You can put this solution on YOUR website!
Answer: 8761324
=====================================================
Explanation:
There are 7 digits, so there are 7! = 7*6*5*4*3*2*1 = 5040 different ways to arrange them. That's a lot of values to check.
We can make life easier by noticing that 44 = 4*11, so the answer must be divisible by 4 and 11. In other words, the answer is a multiple of 4 and a multiple of 11.
The divisibility by 4 rule is that the last two digits are divisible by 4. For example, the number 124 is divisible by 4 because 24 is too. Same for 1324 and 13524. We can have as many digits to the left of "24" and get the same result. This works because after reaching 100, the pattern for the multiples of 4 reset back to 00.
We want to pick the smallest two digit number that is a multiple of 4. Ideally each digit selected, of this two digit number, is as small as possible. The number 12 fits the description here. So we have some number that looks like this
__, __, __, __, __, 1, 2
The blank spaces will be filled with a single digit number from the set {3,4,6,7,8}
Let's try filling in those blank spaces such that we start with 8, then go to 7, and so on counting down til we get to 3. We skip 5 because its not part of the original set.
So we have
__, __, __, __, __, 1, 2
turn into
8, 7, 6, 4, 3, 1, 2
8764312
We already know it is divisible by 4 from the rule mentioned above, but as a check,
8764312/4 = 2191078
is a whole number so we confirm it is divisible by 4. From here on out, I'm only going to check for divisibility by 11 by using this division trick. We dont need to divide for divisibility of 4 checks because we're forcing the last two digits to be multiples of 4.
Check to see if the number is divisible by 11
8764312/11 = 796755.636363637
because we get a non-whole decimal number, we can see that 8764312 is not divisible by 11.
Let's try swapping the 3 and the 1
we go from 8764312 to 8764132 (color used to show which digits swap)
Now check divisibility for 11
8764132/11 = 796739.272727272 is not divisible by 11
----------------------------------------
Let's try having "32" as the last two digits. This is a multple of 4 (because 4*8 = 32). Now have 8 as the first digit, 7 as the second, and so on until you use up the digits.
We have this new number
8764132
Check divisibility for 11
8764132/11 = 796739.272727272 is not divisible by 11
Let's try swapping the 4 and the 1
8764132 ---> 8761432
Check divisibility for 11
8761432/11 = 796739.272727272 is not divisible by 11
----------------------------------------
Back to the drawing board. Let's try having "24" as the last two digits. Arrange the other digits such that we use the largest first, second largest next, and so on until the blank slots are filled. We have this number
8763124
Check for divisibility of 11
8763124/11 = 796647.636363637 doesnt work
Let's try swapping the 3 and the 1 again
8763124 ---> 8761324
Check for divisibility of 4 and 11
8761324/11 = 796484
We finally get a whole number result. This means the number is a multiple of 11.
The value 8761324 is a multiple of 4 and a multiple of 11. So it is a multiple of 4*11 = 44.
As you can see this trial-and-error process is a bit lengthy and we got lucky in terms of finding a multiple of 44 that fit the description in the instructions. This is the largest such number because I forced the left most digits to be as large as possible.
There are other possible permutations of the digits {1,2,3,4,6,7,8} that are multiples of 44. If you are curious what they are, then check out the pastebin link below. I used pastebin so that I could save space on this current page to avoid clutter (the solution is already a bit too long as it is).
pastebin link
https://pastebin.com/qXYy9Skb
There is probably a much more efficient way to do this, but that is escaping me at the moment.
|
|
|
