Question 1150834: The sum of the first ten terms of a linear sequence is -60 and the sum of the first fifteen terms of the sequence is -165.find the 18th term of the sequence
Found 3 solutions by greenestamps, MathLover1, MathTherapy:
Answer by greenestamps(13209)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! linear sequences are sequences where the difference between successive terms is always the same
In General we could write an arithmetic sequence like this:
 , , 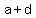 , , 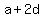 , , 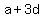 , ... , ...
The sum of the first  terms of an arithmetic sequence use this formula: terms of an arithmetic sequence use this formula:
 where where  is the first term, is the first term,  the number of terms, and the number of terms, and  is common difference is common difference
given:
The sum of the first ten terms of a linear sequence is  ; so, we have ; so, we have
 ........... ten terms=> ........... ten terms=>





 ..................eq.1 ..................eq.1
and the sum of the first fifteen terms of the sequence is 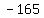
 ........... 15 terms=> ........... 15 terms=>




 .................eq.2 .................eq.2
from eq.1 and eq.2 we have




find first term:
 .................eq.2 .................eq.2



find the 18th term of the sequence:
 , ,  , and , and 




so, your sequence is:
 , , , , , , , , , , , , , , , , , , , ,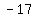 , ,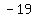 , ,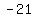 , ,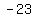 , , , , , ,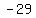 , , ,.... ,....
Answer by MathTherapy(10556)   (Show Source): (Show Source):
|
|
|