Question 1150805: Please help me solve this question: A family plans to have 3 children. Determine the probability that the family will have exactly 1 boy, given that the second child is a boy .
Found 5 solutions by greenestamps, MathLover1, Alan3354, MathTherapy, ikleyn:
Answer by greenestamps(13209)   (Show Source): (Show Source):
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We have 3 children, with each one possibly being a boy or a girl.
And so for each child, the probability of being a boy is  as is the probability of being a girl as is the probability of being a girl  . .
the possible outcomes are
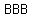 , ,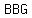 , ,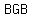 , , , , , , , , , ,
There are  possible outcomes, all equally likely (if we assume each gender is equally likely). possible outcomes, all equally likely (if we assume each gender is equally likely).
What is the probability that all three children in a family will be the same gender?
 (all female)= (all female)= 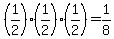
 (all male ) = (all male ) = 
 (all one gender) = (all one gender) = (all female) + (all female) +  (all male) = (all male) =
the probability that the family will have exactly  boy, given that the boy, given that the 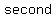 child is a child is a  , is: , is:

Answer by Alan3354(69443)   (Show Source): (Show Source):
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website! Please help me solve this question: A family plans to have 3 children. Determine the probability that the family will have exactly 1 boy, given that the second child is a boy .
From the 8 outcomes, 4 (BBB, BBG, GBB, GBG) are outcomes that involve having a boy as the 2nd child. From this list, ONLY 1 will be EXACTLY 1 boy,
with the 2nd child being a boy (GBG). Therefore, 
OR
Use the CONDITIONAL FORMULA: 
P(1 BOY|2nd is a BOY) =  = = 
I don't know why that person thought this problem was incomplete. I don't know what he's looking at.
The other person, I don't know what she was thinking either, with an answer of 3/8. They BOTH don't make any sense!!
Answer by ikleyn(52886)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The problem can be solved by various ways.
Solution 1. Make and use the sample space directly and explicitly.
The sample space is
BBB BBG BGB BGG GBB GBG GGB GGG
(by coding B = boy, G = girl).
All outcomes are equally likely with the probability of 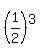 = =  each.
The number of outcomes with a boy as a second child is 4 (BBB BBG GBB GBG).
Of them, the number of outcomes with only one boy in the family is 1 (GBG).
Hence, the probability under the question is P = each.
The number of outcomes with a boy as a second child is 4 (BBB BBG GBB GBG).
Of them, the number of outcomes with only one boy in the family is 1 (GBG).
Hence, the probability under the question is P =  . .
Solution 2. Logical analysis.
If the boy (B) is in the 2-nd of the 3 positions, then for the 1-st and for 3-rd position only G is possible.
Each G at the 1-st position and each G at the 3-rd position goes with the probability of  .
Hence, the probability to have G at the 1-st and 3-rd positions, under the condition, that the 2-nd position is B, is .
Hence, the probability to have G at the 1-st and 3-rd positions, under the condition, that the 2-nd position is B, is  = =  . .
In both solutions, you have the same ANSWER :
the probability under the question is  . .
------------
Solved, answered, and explained.
|
|
|