|
Question 1150775: For what value of k does the following system of equations have one or more solutions?
x - 2y + 2z = 3
-x + 6y + 6z = 1
2x - 7y - 2z = k
1
-2
3
-4
Found 2 solutions by ikleyn, jim_thompson5910:
Answer by ikleyn(52901)   (Show Source):
You can put this solution on YOUR website! .
x - 2y + 2z = 3 (1)
-x + 6y + 6z = 1 (2)
2x - 7y - 2z = k (3)
Add equations (1) and (2). You will get
4y + 8z = 4, or, equivalently,
y + 2z = 1. (4)
Multiply equation (2) by 2 and then add to equation (3). You will get
5y + 10z = 2 + k, or, equivalently,
y + 2z = 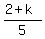 . (5)
Now compare equations (4) and (5). They are compatible if and only if
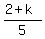= 1, which is equivalent to
2 + k = 5,
k = 5 - 2 = 3. ANSWER
Solved.
Answer by jim_thompson5910(35256)  (Show Source):
You can put this solution on YOUR website!
Convert the system into an augmented matrix. Then row reduce until the matrix is into Row Echelon Form (REF)
The last row has nearly all 0's in it except for the last entry that has -3+k
This means we have
0x + 0y + 0z = -3+k
which is equivalent to
0 = -3+k
Solving for k leads to
0 = -3+k
-3+k = 0
k+(-3) = 0
k-3 = 0
k-3+3 = 0+3
k = 3
If k = 3, then the equation 0 = -3+k is true.
So the row
0x + 0y + 0z = -3+k
will turn into
0x + 0y + 0z = -3+3
0x + 0y + 0z = 0
0 = 0
which is a true statement
If k is anything else but 3, then the equation 0x + 0y + 0z = -3+k will be false and the overall system will be inconsistent.
Final Answer: 3
|
|
|
| |
