|
Question 1150758: A series of 567 consecutive integers has a sum that is a perfect cube. Find the smallest possible positive sum for this series.
Found 3 solutions by MathLover1, ikleyn, MathTherapy:
Answer by MathLover1(20850)   (Show Source): (Show Source):
Answer by ikleyn(52890)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let m+1, m+2, m+3, . . . . , n be a series of 567 consecutive integers with the sum of 567, with the first term (m+1),
where m is a positive integer, and the last term n, n > m.
Then
 - - 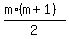 = =  using the formula of the sum of the first positive integer numbers, with some integer positive k.
The formula (1) implies
using the formula of the sum of the first positive integer numbers, with some integer positive k.
The formula (1) implies
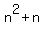 - -  = = 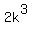
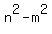 + +  = = 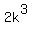 (n-m)*(n+m) + (n-m) =
(n-m)*(n+m) + (n-m) = 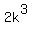 (n-m)*(n+m+1) =
(n-m)*(n+m+1) = 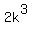 . (2)
Notice that n-m = 567. Thus the formula (2) becomes
567*(n+m+1) = . (2)
Notice that n-m = 567. Thus the formula (2) becomes
567*(n+m+1) = 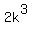 . (3)
The number 567 has the prime decomposition 567 = . (3)
The number 567 has the prime decomposition 567 = 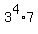 .
Therefore, in order for equation (3) be true with lowest possible value of (n+m-1), it should be
n + m + 1 = .
Therefore, in order for equation (3) be true with lowest possible value of (n+m-1), it should be
n + m + 1 = 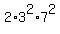 = 882.
Thus we have two equations
n - m = 567, (4)
n + m + 1 = 882. (5)
By adding equations, you get
2n + 1 = 567 + 882 = 1449,
2n = 1449-1 = 1448,
n = 1448/2 = 724.
Then from equation (4), m = 724 - 567 = 157.
Thus the sequence is
158, 159, 160, . . . , 724.
Its sum is = 882.
Thus we have two equations
n - m = 567, (4)
n + m + 1 = 882. (5)
By adding equations, you get
2n + 1 = 567 + 882 = 1449,
2n = 1449-1 = 1448,
n = 1448/2 = 724.
Then from equation (4), m = 724 - 567 = 157.
Thus the sequence is
158, 159, 160, . . . , 724.
Its sum is  = = 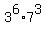 = =  = = 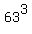 = 250047.
ANSWER. The smallest possible positive sum for this series is = 250047.
ANSWER. The smallest possible positive sum for this series is 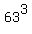 = 250047. = 250047.
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website! A series of 567 consecutive integers has a sum that is a perfect cube. Find the smallest possible positive sum for this series.
Yet, ANOTHER method!!
Sum of an A.P.: 
 ------ Substituting 567 for n, and 1 for d ------ Substituting 567 for n, and 1 for d
 ======> ======>  ======> ======>  =====> =====> 
 ------- Substituting PRIME FACTORS ------- Substituting PRIME FACTORS
 ------ Factoring out GCF, 34 * 7 ------ Factoring out GCF, 34 * 7
From above, it can be seen that a PERFECT CUBE of base 3 would be 36, so ANOTHER 32 is needed (to be MULTIPLIED), and a PERFECT CUBE of base 7 would be 73,
and so, ANOTHER 72 is needed (to be MULTIPLIED) also.
Therefore, for the SMALLEST CUBE, we need to have: 36 * 73, or  , which is actually , which is actually  . .
|
|
|
| |