SOLUTION: The sum of the n terms of two arithmetic progression are in the ratio (3n+8):(7n+15). Find the ratio of their 12th terms

Our APs (arithmetic progressions) are

    a,  a+d,  a+2*d,  a+3*d, . . . 

    b,  b+e,  b+2*e,  b+3*e, . . . 

where  "a"  and  "b"  are first terms  and  "d"  and  "e"  are their common differences.   


In order for to answer the question, it is enough to know three ratios  ,    and  .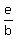

So, our goal now is to find these three ratios.



1)  At n= 1  we have


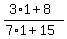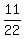         =  =  = .         (1)  



2)  At n= 2  we have


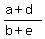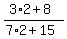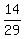         =  = ,  or

        29*(a+d) = 14*(b+e),

        29a + 29d - 14e = 14b.


    Divide both sides by "b" 

        29*(a/b) + 29*(d/b) - 14*(e/b) = 14.


    Substitute here  =  from (1) and multiply both sides by 2. You will get then

        58*(d/b) - 28*(e/b) = -1.       (2)



3)  At n= 3  we have


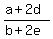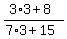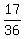         =  = ,  or

        36*(a+2d) = 17*(b+2e),

        36a + 72d - 34e = 17b.


    Divide both sides by "b" 

        36*(a/b) + 72*(d/b) - 34*(e/b) = 17.


    Substitute here  =  from (1). You will get then

        72*(d/b) - 34*(e/b) = -1.       (3)



4)  Introduce new variables  D =   and  E = 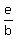.  For these unknowns, from (2) and (3) you have this system of equations

        58*D - 28*E = -1        (2')

        72*D - 34*E = -1        (3')

    Solve it by any method you want / (you know).  The solution is  D = 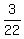,  E = .  Thus   = ,   = .



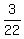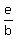5)  Now we are in position to calculate 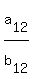  = 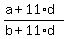 =  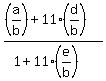=  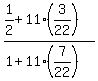=  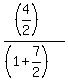= .    ANSWER