SOLUTION: the sides of a triangle measure 21m, 27m, and 36m. a circle is drawn such its center lies on the 21m side and tangent to the remaining sides. find the radius of the circle.

Algebra ->  Customizable Word Problem Solvers  -> Numbers -> SOLUTION: the sides of a triangle measure 21m, 27m, and 36m. a circle is drawn such its center lies on the 21m side and tangent to the remaining sides. find the radius of the circle.      Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 1150481: the sides of a triangle measure 21m, 27m, and 36m. a circle is drawn such its center lies on the 21m side and tangent to the remaining sides. find the radius of the circle.
Answer by ikleyn(52806) About Me  (Show Source):
You can put this solution on YOUR website!
.

            This problem is to be solved in two steps.


Step 1 

Find the area of the triangle using the Heron's formula.


The perimeter is  P = 21+27+36 = 84 meters;  semi-perimeter is 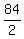84%2F2 = 42 meters.


According to the Heron's formula, the area of the triangle is


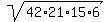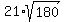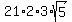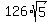    sqrt%2842%2A%2842-21%29%2A%2842-27%29%2A%2842-36%29%29 = sqrt%2842%2A21%2A15%2A6%29 = 21%2Asqrt%28180%29 = 21%2A2%2A3%2Asqrt%285%29 = 126%2Asqrt%285%29  square meters.


Step 2 

In the given triangle, connect the center of the semi-circle with the opposite vertex.


This segment will divide the given triangle in two smaller triangles.


For these smaller triangles, their bases are the sides of the length of 27 and 36 meters. The altitudes drawn to these bases 

from the center of the semi-circle, are the radii of the semicircle.


So the area of the given triangle is equal to the sum of areas of the smaller triangles


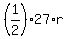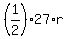    area = %281%2F2%29%2A27%2Ar + %281%2F2%29%2A36%2Ar.


Thus you have this equation


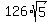    %281%2F2%29%2A27%2Ar + %281%2F2%29%2A36%2Ar = 126%2Asqrt%285%29.


It implies

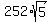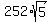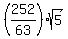    27r + 36r = 252%2Asqrt%285%29,   63r = 252%2Asqrt%285%29,   r = %28252%2F63%29%2Asqrt%285%29 = 4%2Asqrt%285%29 = 8.944 meters (approximately).


ANSWER.  The radius of the circle is  4%2Asqrt%285%29 = 8.944 meters (approximately).

Solved.