Question 1150464: Find the tenth term of a geometric sequence if the third term is 24 and the fifth term is 32/3.
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39620)   (Show Source): (Show Source):
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The "solution" by @josgarithmetic, giving the unique value of  to the common ratio, is UNCOMPLETED, to the common ratio, is UNCOMPLETED,
and, therefore, INCORRECT.
I came to bring the correct solution.
 = 24 = 24
 = = 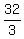
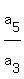 = r^2 = = r^2 = 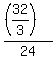 = = 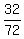 = =  , where r is the common ratio of the progression.
Therefore, the common ratio r may have TWO possible values, r = , where r is the common ratio of the progression.
Therefore, the common ratio r may have TWO possible values, r =  and r = and r =  .
Therefore, looking for .
Therefore, looking for  , we should consider TWO cases.
Case 1. r = , we should consider TWO cases.
Case 1. r =  . Then . Then  = = 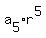 = =  = = 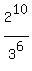 .
Case 2. r = - .
Case 2. r = -  . Then . Then  = = 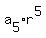 = = 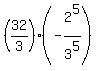 = - = - 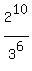 .
ANSWER. Under given conditions, the 10-th term, .
ANSWER. Under given conditions, the 10-th term,  , may have one of the two values , may have one of the two values
 = = 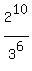 or or  = - = - 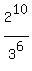 . .
Solved.
|
|
|