Question 1150460: A container filled with 30 litres of wine had 5 litres of the wine removed. To fill the container, 5 liters of water was added. The next day 12 litres of the mixture was removed, and replaced with an equal amount of water. What fraction of the final mixture was water?
Found 2 solutions by jim_thompson5910, ikleyn:
Answer by jim_thompson5910(35256)   (Show Source):
You can put this solution on YOUR website!
Step 1) Remove 5 liters of wine.
Mix A: 30 L of wine, 0 L of water
Mix B: 25 L of wine, 0 L of water
--------------------------------------------------
Step 2) Add 5 liters of water.
Mix B: 25 L of wine, 0 L of water
Mix C: 25 L of wine, 5 L of water
Once we get to mix C, the fractional amount of wine is 5/6 because
25/30 = 5/6
The first fraction is in the form A/B
where
A = amount of wine in liters
B = total amount of mixture (water+wine)
The second fraction is the reduced version of 25/30.
--------------------------------------------------
Step 3) Remove 12 liters of liquid (from mix C)
5/6 of the amount of mix C is composed of wine. So 5/6 of the amount of stuff we remove (12 L) is expected to be wine. The rest is water.
5/6 of 12 = (5/6)*12 = 10 liters of wine is removed
12-10 = 2 liters of water is removed as well
Mix C: 25 L of wine, 5 L of water
Mix D: 15 L of wine, 3 L of water
Going from mix C to mix D, I removed 10 liters of wine and removed 2 liters of water
--------------------------------------------------
Step 4) Add 12 liters of pure water
Mix D: 15 L of wine, 3 L of water
Mix E: 15 L of wine, 15 L of water
(15 L of water)/(15 L of water+15 L of wine) = 15/30 = 1/2 of mix E is water
Answer: 1/2
Answer by ikleyn(52775)  (Show Source):
You can put this solution on YOUR website! .
How about this short version ?
After day 1, you have 30 liters of mixture, containing 25 liters of wine and 5 liters of water.
The proportion water to total is  =  in volumes.
When next day 12 liters of the mixture was removed, 30-12 = 18 liters of mixture remained in the container.
These 18 liters of the mixture contain volume of water, i.e. 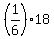 = 3 liters of water.
When 12 liters of water was added, then the total volume of water in the mixture became 3 + 12 = 15 liters.
Thus final fracture of water is  =  of the total volume. ANSWER
-------------------
Surely, it is the same solution as by Jim, only presented in other form.
Now, when you have one long and one short presentation, you can choose which is better for you.
My personal opinion is that IF the shorter solution does not lose nothing essential, THEN it is better.
But you may think differently . . .
Some people understand text much better, when it is shorter.
In short version, I can express, highlight and explain the main ideas MUCH BETTER than ANYONE ELSE in long version.
Regarding long versions, I am 129% sure that NOBODY even reads them,
and 179% sure that nobody understands them, even if read them.
|
|
|
