|
Question 1150428:
Case Study - Planning Ahead
Precision Machining Corporation has been growing steadily over the past decade. Demand for the company’s products continues to rise, so management has decided to expand the production facility; $2 800 000 has been set aside for this over the next four years.
Management has developed two different plans for expanding over the next four years: Plan A and Plan B. Plan A would require equal amounts of $750 000, one year from now, two years from now, three years from now, and four years from now. Plan B would require $300 000 now, $700 000 one year from now, $900 000 two years from now, and $975 000 four years from now.
The company has decided to fund the expansion with only the $2 800 000 and any interest it can earn on it. Before deciding which plan to use, the company asks its treasurer to predict the rates of interest it can earn on the $2 800 000. The treasurer expects that Precision Machining Corporation can invest the $2 800 000 and earn interest at a rate of 4.5% p.a. compounded semi-annually during Year 1, 5.0% p.a. compounded semi-annually during Years 2 and 3, and 5.5% p.a. compounded semi-annually during Year 4. The company can withdraw part of the money from this investment at any time without penalty.
Questions
1.
a. Could Precision Machining Corporation meet the cash requirement of Plan A by investing the $2 800 000 as described above? (Use “now” as the focal date.)
b. What is the exact difference between the cash required and the cash available from the investment?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the details of the transactions are shown below.
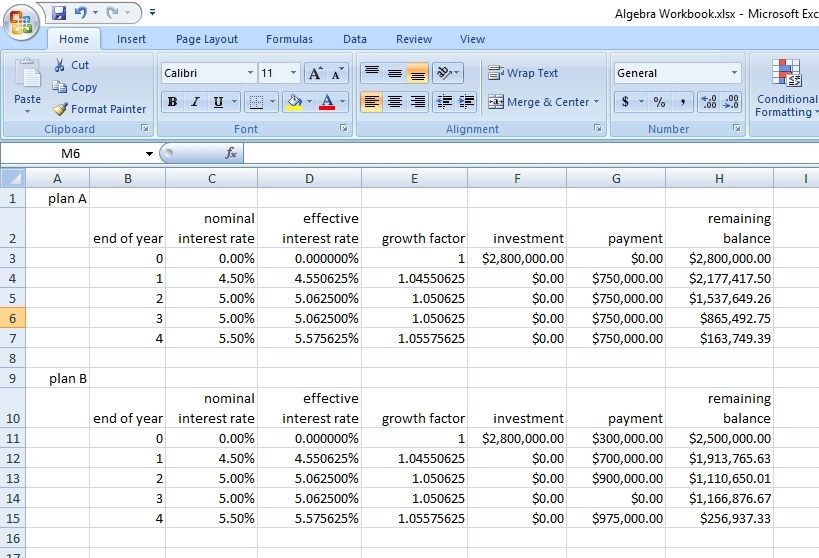
the interest rates given are nominal interest rates.
to find the effective interest rates, you would do the following.
r% = the nominal annual interest rate percent.
r = the nominal annual interest rate percent divided by 100.
c = the number of compounding periods per year.
e = the effective annual interest rate = (1 + r/c) ^ c - 1.
e% = the effective annual interest rate times 100.
g = the effective annual growth factor = 1 + e.
for example, when the nominal annual interest percent is 5% and the interest rate is compounded semi-annually, you get:
r% = 5%
r = 5% / 100 = .05
c = 2
e = (1 + .05/2) ^ 2 - 1 = .050625
e% = e * 100 = 5.0625%
g = 1 + e = 1.050625
the end of year 0 is the beginning of the investment period.
except for the end of year 0 (the beginning of the investment period), the remaining balance for the previous time period is multiplied by the effective annual growth factor for that time period plus any additional investment in that time period minus any payments made in that time period.
the remaining balance at the end of year 0 i simply tne investment minus any payments made at that time.
for example:
for plan A, the remaining balance in time period 2 ($1,537,649.26) is multiplied by the effective annual growth factor for time period 3 (1.050625) plus any additional investment in time period 3 ($0.00) minus any payments in time period 3 ($750,000.00).
that makes the remaining balance in time period 3 equal to $1,537,649.26 * 1.050625 + $0.00 - $750,000.00 = $865,492.75
answers to your questions.
for each year, the remaining balance tells you the cash available while the payment required tells you the cash required.
both plans can meet the the cash requirements for each year of the investment period.
plan B, however, has more cash remaining in the account after all bills have been paid than plan A.
|
|
|
| |