SOLUTION: How much should be invested each year for 10 years to provide you with $6000 per year for the next 15 years? Assume a 5.1% interest rate. (Round your final answer to two decimal pl

   
              How much should you deposit at the end of each year during 10 years to provide you with $6000 per year 
              (at the beginning of each year) for the next 15 years ? Assume a 5.1 interest rate compounding annually.

First, I will determine how much money X should be accumulated on the account during 10 years to the time  of retiring,
in order for to have enough to withdraw $6000 at the beginning of each year for 15 years.


By withdrawing $6000 each year, the compound account (the remaining money) still earns 5.1% per annum,  so everything works as it was 

considered/described at the lesson  Withdrawing a certain amount of money periodically from a compounded saving account  in this site.


Thus the formula for the account value before it starts recharging is

    M = 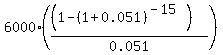,     (1)


which gives us the value at the account 

    M  = 61859.12 dollars.

Now I am in position to determine how much should be deposit at the end of each year during 10 years to the starting moment of the retiring
to accumulate  61859.12 dollars in the account. 


It is the standard Annuity saving plan, and the formula is

    61859.12 = ,     (2)


where D is the annual deposit amount.


The multiplier 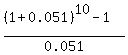  = 12.63776


which implies from equation (2)  that  D =  = 4894.79.


It is your answer:  During 10 years, you should deposit $4894.79 at the end of each year to your account,

                    in order to have the income of $6000 annually from yours account for 15 years, ast the beginning of each year.