Question 1150241: A cross-country skier practices the same route from his home to his friend’s home and leaves at the same time every day. He realised that when he skis at 10 mph he arrives at 4 minutes past noon, and when he skis at 15 mph he arrives at 4 minutes before noon. How fast would he have to go to reach his friend’s house at noon exactly?
Found 2 solutions by ikleyn, VFBundy:
Answer by ikleyn(52767)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let d be the one way distance to ski (in miles).
When the skier skis at the speed of 10 mph, his time is  hours to complete the distance.
When the skier skis at the speed of 15 mph, his time is hours to complete the distance.
When the skier skis at the speed of 15 mph, his time is  hours to complete the distance.
According to the condition, hours to complete the distance.
According to the condition,
 - -  = =  .
The ratio .
The ratio  in the right side of this equation is the time between "4 minutes past noon" and 4 minutes before noon",
expressed in hours.
Solve the equation for "d". For it, multiply both sides by 60: in the right side of this equation is the time between "4 minutes past noon" and 4 minutes before noon",
expressed in hours.
Solve the equation for "d". For it, multiply both sides by 60:
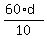 - -  = = 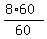 6d - 4d = 8,
d = 4 miles.
Thus the distance is 4 miles.
Now I am in position to answer the problem's question.
At the rate 10 mph, the skier covers 4 miles distance in
6d - 4d = 8,
d = 4 miles.
Thus the distance is 4 miles.
Now I am in position to answer the problem's question.
At the rate 10 mph, the skier covers 4 miles distance in  of an hour, which is 24 minutes.
At this rate, the skier finishes 4 minutes past noon.
To finish exactly at noon, the skier should cover the distance in 24-4 = 20 minutes, or in of an hour, which is 24 minutes.
At this rate, the skier finishes 4 minutes past noon.
To finish exactly at noon, the skier should cover the distance in 24-4 = 20 minutes, or in  of an hour.
Then his rate should be of an hour.
Then his rate should be 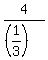 mph = 12 mph.
Answer. To finish at noon, the average speed of the skier should be 12 mph. mph = 12 mph.
Answer. To finish at noon, the average speed of the skier should be 12 mph.
Solved.
---------------
To see other similar solved problems, look into the lesson
- How far do you live from school?
in this site.
Answer by VFBundy(438)   (Show Source): (Show Source):
You can put this solution on YOUR website! Remember that you have to express the time in hours, since you are dealing with miles per hour. In the text to the problem, MINUTES are used. This must be converted to HOURS.
We want the Time (t) to be when the skier finishes exactly at noon. Set up the two scenarios where the skier skis at different speeds.
In the first scenario (10 mph), he finishes at four minutes after noon. Therefore, his Time (t) is expressed as 't + 4/60'. (Remember, four minutes must be expressed in terms of hours.) That fraction can be reduced to 1/15; therefore, when the skier skis at 10 mph, his Time is: t + 1/15.
In the second scenario (15 mph), he finishes at four minutes before noon. Therefore, his Time (t) is expressed as 't - 4/60'. Again, the fraction can be reduced; therefore, when the skier skis at 15 mph, his Time is: t - 1/15.
Here are the two different scenarios. Remember that Distance = Rate * Time, so the Distance in each scenario will be written as Rate * Time.
Skiing 10 mph:
Distance = 10(t + 1/15) = 10t + 2/3
Rate = 10
Time = t + 1/15
Skiing 15 mph:
Distance = 15(t - 1/15) = 15t - 1
Rate = 15
Time = t - 1/15
In each scenario, the Distance is obviously the same, so...:
10t + 2/3 = 15t - 1
-5t = -5/3
t = 1/3
So, we now know that t = 1/3. (Remember, this is in hours.) Using either of the Distances from earlier (it doesn't matter which), calculate the Time (t):
10t + 2/3 = 10(1/3) + 2/3 = 10/3 + 2/3 = 12/3 = 4
You can also use the 'other' Distance:
15t - 1 = 15(1/3) - 1 = 5 - 1 = 4
Just to show you, either way, the Distance is 4.
So, we know the Distance is 4, and we know the Time (t) is 1/3. (Remember, 't' is the time it takes for the skier to arrive exactly at noon.) To find the Rate when the skier arrives exactly at noon, use the formula:
Rate = 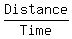 = =  = 12 = 12
So, the skier must ski at 12 mph to arrive at his friend's house exactly at noon.
|
|
|