Question 1150214: In 1991, the moose population in a park was measured to be 5800. By 1996, the population was measured again to be 6900. If the population continues to change linearly, find an equation for the moose population, P, as a function of t, the years since 1988.
What does your model predict the moose population to be in 2006?
Found 2 solutions by ankor@dixie-net.com, MathTherapy:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! In 1991, the moose population in a park was measured to be 5800.
By 1996, the population was measured again to be 6900.
If the population continues to change linearly, find an equation for the moose population, P, as a function of t, the years since 1988.
x = no. of yrs since 1988
y = no. mooses, meeses??
:
x1=3, y1=5800
x2=8, y2=6900
find the slope m = 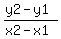
m =  = =  = 220 is the slope = 220 is the slope
:
Use the point slope equation: y - y1 = m(x - x1)
y - 5800 = 220(x - 3)
y = 220x - 660 + 5800
y = 220x + 5140
:
What does your model predict the moose population to be in 2006?
x: 2006 - 1988 = 18
y = 220(18) + 5140
y = 3960 + 5140
y = 9100 meese
:
"P, as a function of t,"
p(t) = 220t + 5140
Answer by MathTherapy(10557)   (Show Source): (Show Source):
You can put this solution on YOUR website! In 1991, the moose population in a park was measured to be 5800. By 1996, the population was measured again to be 6900. If the population continues to change linearly, find an equation for the moose population, P, as a function of t, the years since 1988.
What does your model predict the moose population to be in 2006?
Are you serious, @ANKOR? What are MEESE/MEESES/MOOSES?
I can't believe one would attach such words to his/her response! This MUST be a joke!
|
|
|