Question 1150087: f(x) = (x - 7)^2, x ≥ 7
find the inverse of the function
Found 2 solutions by greenestamps, Theo:
Answer by greenestamps(13198)   (Show Source): (Show Source):
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! function is:
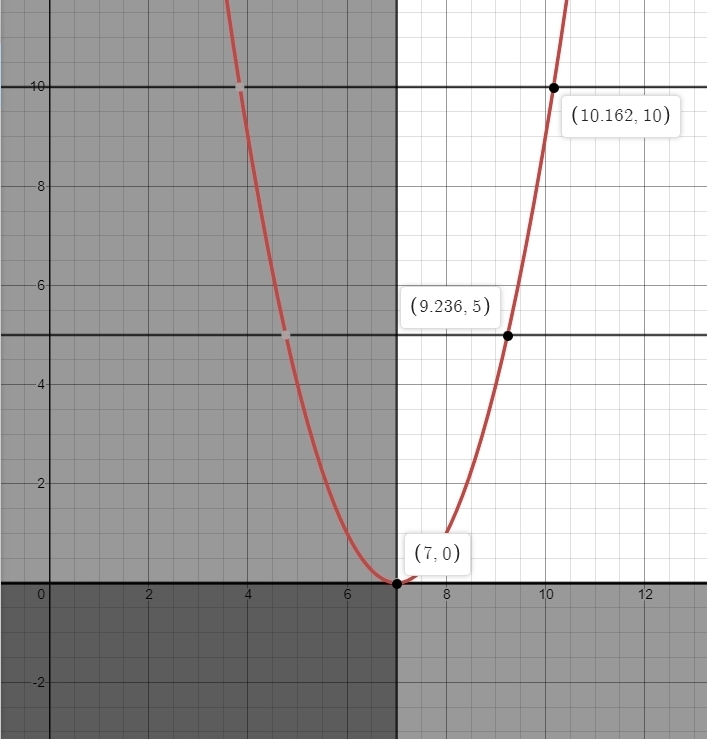
f(x) = (x - 7) ^ 2, x >= 7
the domain is all values of x >= 7
the range is all values of y >= 0
the graph of that function looks like this:
set y = f(x).
replace y with x and x with y to get:
y = (x - 7) ^ 2 becomes:
x = (y - 7) ^ 2
take the square root of both sides of the equation to get:
plus or minus sqrt(x) = y - 7
add 7 to both sides of the equation to get:
7 plus or minus sqrt(x) = y
the domain is all values of x >= 0
the range is all values of y >= 7
for all values of y >= 7, the inverse function of y = plus sqrt(x) is the only one used.
set y = g(x) and it becomes g(x) = 7 + sqrt(x).
here's what it looks like.
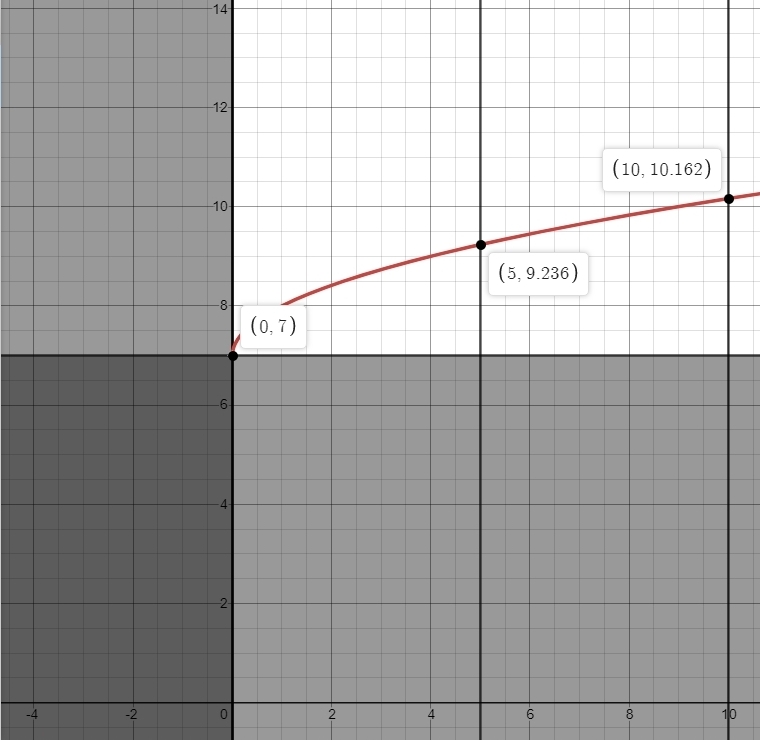
your original function if f(x) = (x - 7) ^ 2
your inverse function is g = 7 + sqrt(x).
the domain of the original function becomes the range of the inverse function function.
the range of the original function becomes the domain of the inverse function.
f(x,y) of the original function becomes g(y,x) in the inverse function.
the graph of the inverse function is a reflection of the original function about the line y = x.
you can see that the point (7,0) in the original graph becomes the point (0,7) in the inverse graph, and that the point (9.236,5) in the original graph becomes the point (5,9.236) in the inverse graph, and that the point (10.162,10) in the original graph becomes the point (10,10.162) in the inverse graph.
you can also plot both equations on the same graph where you can see that f(x,y) = g(y,x) visually, as shown below:
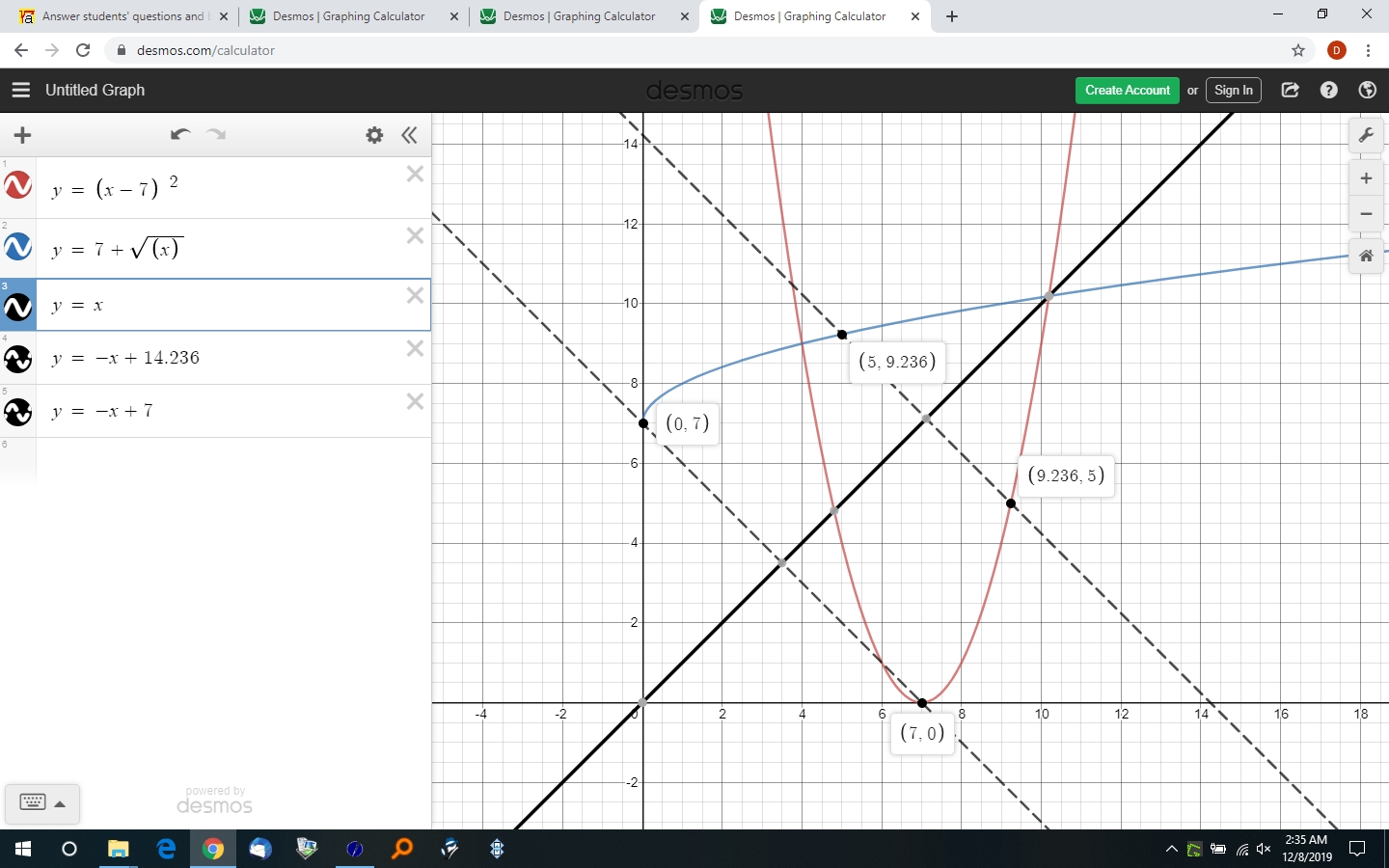
you can see that the point (7,0) on the original graph (shown in red) is a reflection about the line y = x of the point (0,7) on the inverse graph (shown in blue).
you can also see that the point (9.236,5) on the original graph is a reflection about the line y = x of the point (5,9.236) on the inverse graph
when you look at this last graph, you need to make all values of the red line disappear in your mind when x < 7, because that part of the red line graph should not be shown.
this could be done if you manually graphed the equation, but it can't be done using the mechanically generated graph that i did.
the solution to your problem is that the inverse to the function f(x) = (x - 7) ^ 2, where x >= 7 and y >= 0, is g(x) = 7 + sqrt(x), where x >= 0 and y >= 7.
since g(x) is the inverse to f(x), then g(x) can be also be called f^-1(x).
here's a reference on inverse functions.
http://www.themathpage.com/aPreCalc/inverse-functions.htm
|
|
|