Question 1150079: If (a)(b^4)(c^3)=1215000, where a, b and c are distinct positive integers greater than 1, what is the greatest possible value of a+b+c.
Found 3 solutions by ikleyn, MathTherapy, greenestamps:
Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The prime decomposition of the number 1215000 is
1215000 =  . .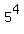 . . .
Comparing it with .
Comparing it with  , you see that
either a= 3^5, b= 5, c= 2, with a+b+c = 3^5 + 5 + 2 = 250,
or a= 3^2, b= 5, c = 2*3, with a+b+c = 3^2 + 5 + 2*3 = 20,
or a = 3, b= 5*3, c = 2, with a+b+c = 3 + 5*3 + 2 = 20.
So, a+b+c is maximal and equal to 250 at a= 3^5, b= 5 and c= 2. ANSWER , you see that
either a= 3^5, b= 5, c= 2, with a+b+c = 3^5 + 5 + 2 = 250,
or a= 3^2, b= 5, c = 2*3, with a+b+c = 3^2 + 5 + 2*3 = 20,
or a = 3, b= 5*3, c = 2, with a+b+c = 3 + 5*3 + 2 = 20.
So, a+b+c is maximal and equal to 250 at a= 3^5, b= 5 and c= 2. ANSWER
Solved.
Answer by MathTherapy(10556)   (Show Source): (Show Source):
Answer by greenestamps(13209)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The prime factorization of 1215000 is (2^3)*(3^5)*(5^4). This is to be expressed as (a)(b^4)(c^3), with the sum a+b+c as large as possible.
Since in that form b and c are small numbers, and since we want the sum a+b+c to be as large as possible, we want a to contain as many large factors as possible.
So we want a to contain all 4 factors of 5.
There are only 3 prime factors of 2 in the number, so b can't be 2. So b should be 3, with c = 2.
Then (b^4)(c^3) = (3^4)(2^3); and then a is made up of the remaining factors of the number: (3^1)(5^4).
So
a = 3*5^4 = 3*625 = 1875
b = 3
c = 2
The maximum sum a+b+c is 1875+3+2 = 1880.
|
|
|