.
(1) If 4x-3y - sqrt(4x-3y) = 56, then introduce t = sqrt(4x-3y) and get the equation
t^2 - t = 56, t^2 - t - 56 = 0, (t-8)*(t+7) = 0.
The roots are 8 or -7. In what follows, I will consider only positive value of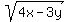 
.
So, sqrt(4x-3y) = 8; hence, 4x - 3y = 64.
(2) Follow by the same way, and from the second equation, 7x-2y + sqrt(7x-2y) = 12 find
t = sqrt(7x-2y), t^2 +t -12 = 0, (t-3)*(t+4) = 0.
Of the two roots for sqrt, take only positive t= 3.
It gives sqrt(7x-2y) = 3; hence 7x - 2y = 9.
(3) Now you have the system of 2 equations in 2 unknowns
4x - 3y = 64,
7x - 2y = 9.
Solve it by any way and any method you know (it is just arithmetic) and find x and y.
(4) Then calculate x-y.
