SOLUTION: The tide on a certain shore on a planet has a period of 36.5 hours, and the high tide level is 8 m above the low tide level. At t = 0 the water level is 2 m above the low tide leve

Algebra ->  Trigonometry-basics -> SOLUTION: The tide on a certain shore on a planet has a period of 36.5 hours, and the high tide level is 8 m above the low tide level. At t = 0 the water level is 2 m above the low tide leve      Log On


   

Question 1150036: The tide on a certain shore on a planet has a period of 36.5 hours, and the high tide level is 8 m above the low tide level. At t = 0 the water level is 2 m above the low tide level and rising. Using trigonometric functions, find a function to describe the height H(t) of the water above the low tide level
Found 3 solutions by josmiceli, Alan3354, jim_thompson5910:
Answer by josmiceli(19441) About Me  (Show Source):
You can put this solution on YOUR website!
+H%28t%29+=+-4%2Acos%28+%28%28+t%2F36.5+%29%2A%28+2pi+%29+%29+%2B+pi%2F3+%29+
(a) The amplitude is +%281%2F2%29%2A8+=+4+
(b) When +t+=+36.5+, the tide is back to starting level of +-2+
(c) When +t+=+0+, +-4%2Acos%28+pi%2F3+%29+=+-2+ and rising
Here is the plot:

-----------------------------------
If needed, get a 2nd opinion, too
======================================================
I asked the doctor for a 2nd opinion, and he said, "OK. You're ugly."

Answer by Alan3354(69443) About Me  (Show Source):
You can put this solution on YOUR website!
I asked the doctor for a 2nd opinion, and he said, "OK. You're ugly."

Answer by jim_thompson5910(35256) About Me  (Show Source):
You can put this solution on YOUR website!

t = number of hours that has elapsed since some starting point
H(t) = height, in meters, of water above the low tide level
H(t) = 8 means we're 8 meters above the low tide level
H(t) = 2 means we're 2 meters above the low tide level
The smallest H(t) can get is 0. The largest is 8.
The range of this trig function is 0+%3C=+H%28t%29+%3C=+8 which is the same as saying 0+%3C=+y+%3C=+8 if y = H(t)

General sine function is
y = A*sin(B(x-C))+D
A = amplitude
B = determined by the period
C = phase shift (aka horizontal shift)
D = vertical shift = midline

Lets find the values for A,B,C,D
A = amplitude
A = half the vertical distance between the lower and upper bounds of the range
A = (upper - lower)/2
A = (8-0)/2
A = 4

P = period = 36.5 hours
B = 2pi/P
B = 2pi/36.5

C = phase shift
We'll come back to this later

D = midline
D = midpoint of upper and lower boundaries of the range
D = (upper+lower)/2
D = (8+0)/2
D = 4

We have
A = 4
B = 2pi/36.5
C = unknown for now
D = 4

So,
y+=+A%2Asin%28B%28x-C%29%29%2BD
turns into
y+=+4%2Asin%28expr%282pi%2F36.5%29%28x-C%29%29%2B4

Let's plug in (x,y) = (0,2) to indicate we want the starting water level to be 2 meters.
In other words, we want H(t) = 2 when t = 0.
Now solve for the variable C
y+=+4%2Asin%28expr%282pi%2F36.5%29%28x-C%29%29%2B4
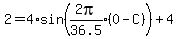
2+=+4%2Asin%28expr%282pi%2F36.5%29%280-C%29%29%2B4
2-4+=+4%2Asin%28expr%282pi%2F36.5%29%28-C%29%29
-2+=+4%2Asin%28-expr%282pi%2F36.5%29C%29
4%2Asin%28-expr%282pi%2F36.5%29C%29+=+-2
sin%28-expr%282pi%2F36.5%29C%29+=+-2%2F4
sin%28-expr%282pi%2F36.5%29C%29+=+-1%2F2
-expr%282pi%2F36.5%29C+=+arcsin%28-1%2F2%29
-expr%282pi%2F36.5%29C+=+-pi%2F6
expr%282%2F36.5%29C+=+1%2F6
C+=+%2836.5%2F2%29%2A%281%2F6%29
C+=+18.25%2A%281%2F6%29
C+=+18.25%2F6
We can update
y+=+4%2Asin%28expr%282pi%2F36.5%29%28x-C%29%29%2B4
into
y+=+4%2Asin%28expr%282pi%2F36.5%29%28x-18.25%2F6%29%29%2B4
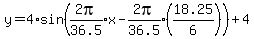
y+=+4%2Asin%28expr%282pi%2F36.5%29x-expr%282pi%2F36.5%29%2A%2818.25%2F6%29%29%2B4
y+=+4%2Asin%28expr%282pi%2F36.5%29x-pi%2F6%29%2B4
H%28t%29+=+4%2Asin%28expr%282pi%2F36.5%29t-pi%2F6%29%2B4

-------------------------------------------------------------------------------

Final Answer:
H%28t%29+=+4%2Asin%28expr%282pi%2F36.5%29t-pi%2F6%29%2B4
Graph:

Notes:

  • x = t = elapsed time in hours

  • y = H(t) = height, in meters, of water above the low tide level

  • The sine curve stays between y = 0 and y = 8

  • The graph repeats itself every x = 36.5 units. The water is at a height of y = 2 when x = 0. The water level goes up, comes back down to y = 0, and goes back up again to arrive back at y = 2 when x = 36.5

  • The horizontal distance between any peak to its adjacent neighbor valley is x = 18.25, which is half of the period 36.5

  • The amplitude of 4 represents vertical distance from the midline y = 4 to either the peak (y = 8) or the valley (y = 0).