Question 1150018: A mathematics professor assigns two problems for homework and knows that the probability of a student solving the first problem is 0.85, the probability of solving the second is 0.45, and the probability of solving both is 0.05. (Round your answers to three decimal places.)
(a) Jed has solved the second problem. What is the probability he also solves the first problem?
(b) Edna has solved the first problem. What is the probability she also solves the second problem?
Found 2 solutions by jim_thompson5910, ikleyn:
Answer by jim_thompson5910(35256)   (Show Source): (Show Source):
You can put this solution on YOUR website!
A = event of solving the first problem
B = event of solving the second problem
Given
P(A) = 0.85
P(B) = 0.45
P(A and B) = 0.05
------------------------------------------------
Part (a)
Jed has solved the second problem. So we're given that event B has happened. We want to find P(A|B) which is the probability of event A happening given B has happened.
Use the conditional probability formula
P(A|B) = P(A and B)/P(B)
P(A|B) = 0.05/0.45
P(A|B) = 0.111111
P(A|B) = 0.111
Answer: 0.111
------------------------------------------------
Part (b)
Same idea as in part (a), but now we want to find P(B|A). We know event A has happened and we want to find the probability of event B happening based on A.
P(B|A) = P(B and A)/P(A)
P(B|A) = P(A and B)/P(A)
P(B|A) = 0.05/0.85
P(B|A) = 0.05882
P(B|A) = 0.059
Answer: 0.059
Answer by ikleyn(52848)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This problem is on CONDITIONAL PROBABILITY
Let me re-formulate the problem, to make it (and its solution) more clear.
There is a universal set U of 100 students.
Subset A consists of 85 students.
Subset B consists of 45 students.
Subset (A & B) consists of 5 students // here (A & B) means intersection A and B
(a) Jed is from subset B. what is the probability that Jed belongs to subset A, too ?
In other words, if you take an arbitrary student from B, what is the probability that he / (or she)
does belong to the intersection C = (A & B) ?
The ANSWER is OBVIOUS: the probability P =  = =  .
On the language of conditional probability, you are given P(B) = 0.45, P(A & B) = 0.05, and they ask you about P(A | B).
By the definition of the conditional probability,
P(A | B) = P(A & B) / P(B) = 0.05/0.45 = .
On the language of conditional probability, you are given P(B) = 0.45, P(A & B) = 0.05, and they ask you about P(A | B).
By the definition of the conditional probability,
P(A | B) = P(A & B) / P(B) = 0.05/0.45 = 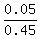 = =  = =  , the same answer.
(b) Having (a) solved by me, try to solve (b) IN THE SAME WAY on your own.
It is VERY similar (!) , the same answer.
(b) Having (a) solved by me, try to solve (b) IN THE SAME WAY on your own.
It is VERY similar (!)
|
|
|