SOLUTION: What is the average rate of change of y with respect to x over the interval [-2,5] for the function y=3x+2

To answer this question, for any function y = y(x) you should calculate its value at the endpoints of the interval y(a) and y(b);

then take the difference y(b)-y(a) and divide it by the difference (b-a)


    average rate of y = ,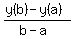


by the definition.  Let's do it for the given function.


    y(b) = y(5) = 3*5+2 = 17;  y(a) = y(-2) = 3*(-2)+2 = -4;

    the difference y(5)-y(2) = 17 - (-4) = 17+4 = 21;

    the difference  5 - (-2) = 7;

    the quotient 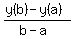  =  = 3.



          So, we just got the ANSWER: average rate of y is equal to 3.



This procedure works for any function y = y(x).


But the given function is SPECIAL : it is LINEAR (!).


For any linear function, its average rate of charge is ALWAYS equal to the slope of the line.

The slope of the given line is 3.  And the average rate of change is 3, also, as we found it above.

So, this rule works in our case, too.


Therefore, if you are given a linear function and somebody asks you about its average rate of change,

you can give the answer quickly without making this boring procedure.


But in general case, you should do it as I explained it for you in my post.