Question 1149891: given that K is the point(t,4) B(1,1) and C(3,4)and the area of triangle BCK is 12 units find the possible values of t.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52824)   (Show Source):
You can put this solution on YOUR website! .
given that K is the point (t,4), B(1,1) and C(3,4) and the area of triangle BCK is 12 units find the possible values of t.
~~~~~~~~~~~~~~~~~~~~
With the given data, the side CK of the triangle is horizontal line y= 4 and has the length of |t-3| units.
The distance from the point B to this horizontal line is 4-1 = 3.
So, the equation for the area of the triangle BCK is
12 =  .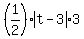
It implies
| t - 3 | = 8,
which has two solutions t= 11 and t= -5.
ANSWER. The possible values of "t" are -5 and 11.
Solved.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
Points C and K are both on the horizontal line x=4, so we can use horizontal segment CK as the base of the triangle.
Since CK is horizontal , the altitude of the triangle is the difference in the y-coordinates of B and C, which is 3.
The area of the triangle, 12, is one-half base times height. That means the length of the base is 8.
So the two values of t for which the area of the triangle is 12 are the two points 8 units right or left from C(3,4).
ANSWERS: 3+8=11 an 3-8 = -5
|
|
|
