.
If x is the side length of the base square and h is the height of the box, then the area of the open box is
A(x,h) =  +
+ 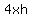 . (1)
The volume of the box is
V(x,h) =
. (1)
The volume of the box is
V(x,h) = 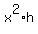 . (2)
We need to minimize the surface area (1) under the restriction
. (2)
We need to minimize the surface area (1) under the restriction
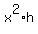 = 62.5 cm^3. (3)
From (3), express h =
= 62.5 cm^3. (3)
From (3), express h = 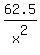 and substitute it into (1). You will get then
A(x) =
and substitute it into (1). You will get then
A(x) =  +
+ 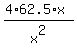 =
=  +
+ 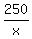 . (4).
Thus we need to minimize function A(x) of one variable "x" expressed by (4).
For it, take the derivative
A'(x) = 2x -
. (4).
Thus we need to minimize function A(x) of one variable "x" expressed by (4).
For it, take the derivative
A'(x) = 2x - 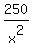 and equate it to 0 (zero). You will get
2x -
and equate it to 0 (zero). You will get
2x - 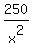 = 0,
2x^3 - 250 = 0,
x^3 = 250/2 = 125,
x =
= 0,
2x^3 - 250 = 0,
x^3 = 250/2 = 125,
x =  = 5 cm.
Then h =
= 5 cm.
Then h = 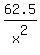 =
= 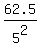 = 2.5 cm.
Thus the optimal dimensions are x = 5 cm; h = 2.5 cm. ANSWER
The surface area of the open box is A =
= 2.5 cm.
Thus the optimal dimensions are x = 5 cm; h = 2.5 cm. ANSWER
The surface area of the open box is A =  + 4*x*h =
+ 4*x*h =  + 4*5*2.5 = 25 + 50 = 75 cm^2. ANSWER
Partial CHECK. The volume =
+ 4*5*2.5 = 25 + 50 = 75 cm^2. ANSWER
Partial CHECK. The volume = 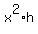 =
= 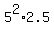 = 62.5 cm^3. ! Correct !
= 62.5 cm^3. ! Correct !
Solved.