Question 1149667: Find the equation of the tangent to the curve y=x+x^2 at the point where x=a find the values of a for which this line passes through the point P(2,-3).Hence find the equation of the tangent from P to the curve.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52847)   (Show Source):
You can put this solution on YOUR website! .
The derivative of the given function is y'(x) = 2x+1; its value at x= a is y'(a) = 2a+1.
The line should go through the points (a,a^2+a) and P(2,-3).
Therefore, the slope of this line is m =  =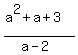 
So, the equation to find the value of "a" is
2a+1 = .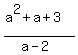
saying that the two expressions for the slope are equal.
Simplify and solve for "a". First step is to multiply both sides by (a-2)
(2a+1)*(a-2) = a^2 + a + 3
2a^2 + a - 4a - 2 = a^2 + a + 3
2a^2 - 3a - 2 = a^2 + a + 3
a^2 -4a - 5 = 0.
(a-5)*(a+1) = 0
The roots are a= 5 and a= -1.
Hence, there are two points on the curve satisfying the given conditions
- one point is (5,30) and the other point is (-1,0),
and two such lines :
- one with the slope of 2*5+1 = 11 and the other with the slope of 2(-1)+1 = -1.
The first line has the equation y+3 = 11*(x-2), or y = 11x - 25.
The second line has the equation y+3 = -(x-2), or y = -x -1.
Plot y = x+x^2 (red), y = 11x-25 (green) and y = -x-1 (blue).
Solved.
Answer by greenestamps(13203)  (Show Source):
You can put this solution on YOUR website!
I do not understand the instructions as you show them for solving the problem, so I will ignore them....
The given function is y = x+x^2.
The derivative of the function is y' = 1+2x.
An arbitrary point on the curve is (a,a+a^2).
The derivative at the point (a,a+a^2) is 1+2a.
We want the slope of the curve at (a,a+a^2) to be equal to the slope between (2,-3) and (a,a+a^2).
 or 
The two points of tangency are where a=5 and where a=-1. Those points are (5,30) and (-1,0).
A graph, showing the points of tangency at x=-1 and x=5.
If you need the equations of the tangent lines, use the two known points (-1,0) and (2,-3) for one of them and the two known points (5,30) and (2,-3) for the other.
|
|
|
