.
Résoudre dans R : Arccos (2x) - Arccos(x) = π/3
~~~~~~~~~~~~~~~~~~~
Arccos (2x) - Arccos(x) = π/3 ===========>
arccos(2x) =  + arccos(x).
Apply cos to both sides.
cos(acrcos(2x)) =
+ arccos(x).
Apply cos to both sides.
cos(acrcos(2x)) =  -
- 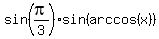 . (1)
Now, part by part,
cos(arccos(2x)) = 2x;
cos(pi/3) =
. (1)
Now, part by part,
cos(arccos(2x)) = 2x;
cos(pi/3) =  ;
cos(arccos(x)) = x;
;
cos(arccos(x)) = x;
 =
=  ;
sin(arccos(x)) =
;
sin(arccos(x)) =  .
Substitute everything into equation (1).
2x =
.
Substitute everything into equation (1).
2x = 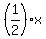 -
- 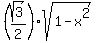 4x = x -
4x = x -  3x = -
3x = -  Square both sides
9x*2 = 3*(1-x^2)
9x^2 = 3 - 3x^2
12x^2 = 3
x^2 =
Square both sides
9x*2 = 3*(1-x^2)
9x^2 = 3 - 3x^2
12x^2 = 3
x^2 = 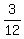 =
=  x = +/-
x = +/-  = +/-
= +/-  .
Now the last step is to check these two candidates.
CHECK.
Case 1. x =
.
Now the last step is to check these two candidates.
CHECK.
Case 1. x =  .
Then 2x = 1, arccos(2x) = arccos(1) = 0 radians.
arccos(x) =
.
Then 2x = 1, arccos(2x) = arccos(1) = 0 radians.
arccos(x) = 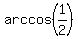 =
=  .
.
 -
-  = -
= -  .
The original equation IS NOT satisfied, so x =
.
The original equation IS NOT satisfied, so x =  IS NOT the solution.
Case 2. x = -
IS NOT the solution.
Case 2. x = -  .
Then 2x = -1, arccos(2x) = arccos(-1) =
.
Then 2x = -1, arccos(2x) = arccos(-1) =  radians.
arccos(x) =
radians.
arccos(x) =  =
=  .
.
 -
-  =
=  .
The original equation IS satisfied, so x = -
.
The original equation IS satisfied, so x = -  IS the solution.
ANSWER. The only solution to the given equation is x = -
IS the solution.
ANSWER. The only solution to the given equation is x = -  .
.
Solved.
-----------------
Come again to the forum soon to learn something new (!)