SOLUTION: 1^2+3^2+...+(2n-1)^2=1/3n(4n^2-1)

Algebra ->  Proofs -> SOLUTION: 1^2+3^2+...+(2n-1)^2=1/3n(4n^2-1)      Log On


   

Question 1149333: 1^2+3^2+...+(2n-1)^2=1/3n(4n^2-1)
Found 2 solutions by ikleyn, math_helper:
Answer by ikleyn(52866) About Me  (Show Source):
You can put this solution on YOUR website!
.

There are several proofs by the method of Mathematical induction.

See the links

https://socratic.org/questions/show-by-induction-that-aa-n-1-1-2-3-2-5-2-2n-1-2-n-3-4n-2-1

https://math.stackexchange.com/questions/623504/prove-that-12-32-2n-12-displaystyle-frac4n3-n3


Happy learning (!)



Answer by math_helper(2461) About Me  (Show Source):
You can put this solution on YOUR website!


n=1:  1%5E2+=+1+   &   %281%2F3%29%281%29%284%281%29%5E2-1%29+=+%281%2F3%29%283%29+=+1+



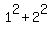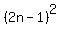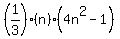Assume 1%5E2%2B2%5E2+ + ... + +%282n-1%29%5E2+ = %281%2F3%29%28n%29%284n%5E2-1%29 for n=k



Let n=k+1:



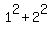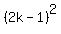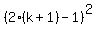
 1%5E2%2B2%5E2+ + ... + +%282k-1%29%5E2+  +  +%282%28k%2B1%29-1%29%5E2+



// Apply hypothesis to all but the last term 

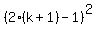
= +%281%2F3%29%28k%29%284k%5E2-1%29+ + +%282%28k%2B1%29-1%29%5E2+



// combine

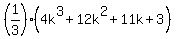
= +%281%2F3%29%284k%5E3%2B12k%5E2%2B11k%2B3%29+



// Here you can attempt to factor, or, you can see if (1/3)(k+1)(4(k+1)^2-1)

// expands to the same expression...  I will do the latter approach...



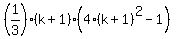
+%281%2F3%29%28k%2B1%29%284%28k%2B1%29%5E2-1%29+

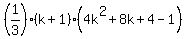
= +%281%2F3%29%28k%2B1%29%284k%5E2%2B8k%2B4-1%29+

= +%281%2F3%29%28k%2B1%29%284k%5E2%2B8k%2B3%29+

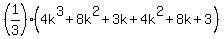
= +%281%2F3%29%284k%5E3%2B8k%5E2%2B3k%2B4k%5E2%2B8k%2B3%29+

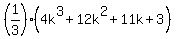
= +%281%2F3%29%284k%5E3%2B12k%5E2%2B11k%2B3%29+



They match, the hypothesis is also true for n=k+1, DONE.