Question 1149313: In a class of 36 students 25 study chemistry and 22 study mathematics and 25
study physics ,17 study physics and mathematics,18 study physics and
chemistry,15 study one of the three subject Find a)Those who study all three
subject b) only mathematics and chemistry
Found 5 solutions by greenestamps, Edwin McCravy, math_helper, AnlytcPhil, ikleyn:
Answer by greenestamps(13198)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The questions that are asked, if the problem is read exactly as written, are impossible to answer.
The problem asks us to "find those who study all 3 subjects" and "find (those) who study only mathematics and chemistry".
The only information given in the problem is the NUMBERS of students that take different courses; there are no names of students given, so it is not possible to know WHICH students take various courses.
Note further that the information given in the problem is open to different interpretations.
(1) The last number given should say that 15 students study ONLY one of the three subjects.
(2) The statement of the problem also should specifically state that there are no students who take none of the three courses, or, alternatively, that each of the 36 students takes at least one of them.
However, the problem AS IT WAS INTENDED TO BE PRESENTED is an interesting one.
There are 7 combinations of at least one of the three subjects Chemistry (C), Mathematics (M), and Physics (P) that a student can take:
CMP
CM
CP
MP
C
M
P
Let x be the number who study all three subjects.
Then "17 study physics and mathematics" means (17-x) study ONLY physics and mathematics
And "18 study physics and chemistry" means (18-x) study ONLY physics and chemistry.
Now, knowing that a total of 25 students study physics, we can find an expression for the number that study ONLY physics.
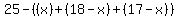 which simplifies to 10-x. which simplifies to 10-x.
At this point, we have nowhere else to go without introducing another unknown.
Let y be the number that study only chemistry and mathematics. Then we can get expressions for the numbers that study only chemistry or only mathematics.
only chemistry: 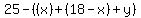 which simplifies to 7-y. which simplifies to 7-y.
only mathematics: 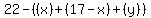 which simplifies to 5-y. which simplifies to 5-y.
We now have expressions for the numbers of students that take each combination of courses:
CMP x
CM y
CP 18-x
MP 17-x
C 7-y
M 5-y
P x-10
-------------
total 37-y
But the total number of students is 36; so y=1.
That means 7-1=6 students take only chemistry and 5-1=4 take only mathematics.
Then since 15 students take only one of the three courses, the number that take only physics is 5. So x-10=5, making x=15. So now
x=15 take all three subjects
18-x=3 take only chemistry and physics
17-x=2 take only mathematics and physics
And now we have all the numbers....
CMP 15
CM 1
CP 3
MP 2
C 6
M 4
P 5
-------------
total 36
ANSWERS:
(a) 15 students study all three courses
(b) 1 student studies only chemistry and mathematics
-------------------------------------------
Added after seeing the solution from the other tutor....
My solution is NOT incorrect. It satisfies all of the given conditions.
It also has every student taking at least one of the three courses. Since the problem doesn't say otherwise, I think that can be assumed.
He came up with a solution to a different problem that satisfies all the given conditions and has 1 student not taking any of the classes....
Answer by Edwin McCravy(20054)   (Show Source): (Show Source):
Answer by math_helper(2461)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Using the same interpretation as tutor @greenestamps, and borrowing the nice Venn diagram code from tutor @Edwin_M, and adding my own lettering:

a = Chem only
b = Chem & Math only
c = Math only
d = all 3 subjects
e = Chem & Phys only
f = Math & Phys only
g = Phys only
There are 7 equations in 7 unknowns:
1. a+c+g = 15
2. e+d = 18
3. f+d = 17
4. a+b+d+e = 25
5. c+b+d+f = 22
6. d+e+f+g = 25
7. a+b+c+d+e+f+g = 36

Which has the solution (courtesy of http://www.bluebit.gr/matrix-calculator/solve.aspx):
a = 6
b = 1 <<< Taking Math & Chem only
c = 4
d = 15 <<< Taking all 3 subjects
e = 3
f = 2
g = 5
This agrees with tutor @greenestamps answer. Tutor @Edwin_McCrary has a at least one setup problem that I noticed: (referring to his diagrams) e + g + i = 15 should be d + f + j = 15.
Best wishes.
Answer by AnlytcPhil(1806)   (Show Source): (Show Source):
You can put this solution on YOUR website! We can solve this, but it contains a very badly-worded ambiguous statement. >>15 study one of the three subjects<<The word "one" could either mean "EXACTLY one" or "ONE or more". >>15 study EXACTLY one of the three subjects<<could give one answer and >>15 study one OR MORE of the three subjects<<
could give another. However, luckily we can tell which it is in this problem.
We can tell that it means "EXACTLY one" because 15 happens to be too small for
"ONE or more" to make sense, because, for instance, there are more than 15 in,
say, the 25 that study chemistry. So luckily we can solve the problem, but you
should point out to your teacher not to just write "one" ever, but always
"EXACTLY one" or "ONE or more". For if you have $5, you have $1, right?
Anyway:
In a class of 36 students 25 study chemistry and 22 study mathematics and 25
study physics, 17 study physics and mathematics, 18 study physics and
chemistry, 15 study one of the three subjects. Find a)Those who study all three
subjects b) only mathematics and chemistry

In a class of 36 students
d+e+f+g+h+i+j+k = 36
25 study chemistry
d+e+g+h = 25
and 22 study mathematics
e+f+h+i = 22
and 25 study physics
g+h+i+j = 25
17 study physics and mathematics
h+i = 17
18 study physics and chemistry
g+h = 18
15 study EXACTLY one of the three subjects
d+f+j = 15
So we line up the equations:
1 d+e+f+g+h+i+j+k = 36
2 d+e +g+h = 25
3 e+f +h+i = 22
4 g+h+i+j = 25
5 h+i = 17
6 g+h = 18
7 d +f +j = 15
This is an "under-determined system" for it has 8 unknowns
but only 7 equations. The determining thing will be the fact
that the solutions must all be non-negative integers.
We use matrix feature of TI-83 or 84. And we get the
answers in terms of k, the number studying none of the three
subjects.
d = 6-k
e = 1+k
f = 4-k
g = 3-2k
h = 15+2k
i = 2-2k
j = 5+2k
Since i = 2-2k ≥ 0
-2k ≥ -2
k ≤ 1
So there are two solutions, k=0 and k=1
Substituting k = 1 in the equations above gives
 Substituting k = 0 in the equations above gives
Substituting k = 0 in the equations above gives
 Find a)Those who study all three subject
That's h, which is 15 for k=0, or 17 for k=1
b) only mathematics and chemistry
That's g, which is 3 for k=0, or 1 for k=1.
The second solution above with k=0 agrees with the other tutors. But I do
consider the first case k=1 to be a legitimate solution as well.
Edwin
Find a)Those who study all three subject
That's h, which is 15 for k=0, or 17 for k=1
b) only mathematics and chemistry
That's g, which is 3 for k=0, or 1 for k=1.
The second solution above with k=0 agrees with the other tutors. But I do
consider the first case k=1 to be a legitimate solution as well.
Edwin
Answer by ikleyn(52772)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a class of 36 students 25 study chemistry and 22 study mathematics and 25 study physics ,17 study physics and mathematics,
18 study physics and chemistry,15 study one of the three subject
Find a)Those who study all three subject b) only mathematics and chemistry
~~~~~~~~~~~~~~~~
The solution by @greenestamps is correct; (G)
The solution by @math_helper is correct; (MH)
The solution by Edwin is NOT CORRECT. (E)
My solution is BELOW. It supports (G) and (MH) and disproves (E).
See also my comments after my solution.
We are given a universal set of 36 students (the entire class).
We are also given info about three its subsets :
C (students enrolled to Chemistry) of n(C) = 25 elements;
M (Mathematics) of n(M) = 22 elements, and
P (Physics) of n(P) = 25 elements.
We are also given the following info about their in-pair intersections:
PM (studying Physics and Math) of n(PM) = 17 elements;
PC (studying Physics and Chemistry) of n(PC) = 18 elements;
MC (studying Math and Chemistry) of n(MC) = unknown number of elements.
We also should find the number of elements in the the triple intersection
PMC (studying Physics, Math and Chem) of n(PMC) (unknown number of elements).
We assume (from the context) that the union of subsets P, M and C is the entire set of the 36 students in the class.
In this situation the following formula works
n(P U M U C) = n(P) + n(M) + n(C) - n(P n M) - n(P n C) - n(M n C) + n(P n M n C). (1)
Substitute the given data. You will get
36 = 25 + 22 + 25 - 17 - 18 - n(MC) + n(PMC), or
n(MC) - n(PMC) = 25 + 22 + 25 - 17 - 18 - 36 = 1.
This difference, n(MC) - n(PMC), is exactly the number of those who study only Math and Chemistry,
so it is just answer to question b) of the problem.
Now we will work to answer question a) and to find the unknown n(PMC).
For it, I should create the other equation, based on the second given condition.
The number of those who study only Math is 22-n(PM)-n(MC)+n(PMC) = 22-n(PM)-(n(MC)-n(PMC)) =
replace here n(PM) by 17 and replace (n(MC)-n(PMC)) by 1, as we just found, to continue the line
= 22-17-1 = 4.
The number of those who study only Physics is 25-n(PM)-n(PC)+n(PMC) = 25-17-18+n(PMC) = -10+n(PMC).
The number of those who study only Chemistry is 25-n(PC)-n(MC)+n(PMC) = 25-n(PC)-(nMC)-n(PMC) =
replace here n(PC) by 18 and replace (n(MC)-n(PMC)) by 1, as we just found, to continue the line
= 25-18-1 = 6.
Now the equation "the sum of those who study only one of the three subjects" is
4 - 10+n(PMC) + 6 = 15, which implies n(PMC) = 15 - 4 + 10 - 6 = 15.
ANSWER to (a) : 15. ANSWER to (b) : 1.
Solved.
-----------------
The last step is to prove the formula (1).
It is totally clear to you why I add the first three addends in the formula (1).
But when I add them, I count twice every term in each in-pair intersection.
Therefore, I subtract the numbers of terms in each in-pair intersection.
Next, when I add three first addends, I count thrice each term in the triple intersection;
and when I subtract in-pair intersections, I cancel these terms thrice.
Therefore, I must add the number of terms in the triple intersection one more time to restore the balance.
Thus the formula (1) is proved // and the solution is completed (! !)
/\/\/\/\/\/\/\/
My comments.
Probably, the formulation is not perfect; probably, it could be better.
But as formulated, it does not leave any doubt/doubts
- that the condition covers and involves all 36 students of the class, and
- what does it mean "15 study one of the three subject".
It is a STANDARD WAY to formulate such circumstances in this sort of problems,
and I saw tens of them in this forum, formulated in this way.
Regarding matrix solutions by Edwin and by @Math_helper, I do not think that it is the expected way for the school students
to get the solution.
It is why I produced my own solution and placed it here.
Thank you for your attention (!)
===================
Dear reader, if you want to see other similar solved problems, to wider your horizon and to feel
the solid ground under your legs, look into the lessons
- Counting elements in sub-sets of a given finite set
- Advanced problems on counting elements in sub-sets of a given finite set
- Challenging problems on counting elements in subsets of a given finite set
in this site.
Look also into the links
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1132870.html
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1129554.html
https://www.algebra.com/algebra/homework/Probability-and-statistics/Probability-and-statistics.faq.question.1129554.html
https://www.algebra.com/algebra/homework/Rate-of-work-word-problems/Rate-of-work-word-problems.faq.question.1126097.html
https://www.algebra.com/algebra/homework/word/evaluation/Evaluation_Word_Problems.faq.question.1126099.html
to similar solved problems in the archive of this forum.
When you learn from these sources, you will know the subject as well, as I know it . . .
|
|
|