SOLUTION: Probability that a student owns a credit card is 0.43. Probability that a student is a freshman is 0.6. Probability that a student owns a credit card and is a freshman is 0.21. Fin

In this problem, the event A is that  "a student owns a credit card".
The probability of this event is  P(A) = 0.43.


The event B is that  "a student is a freshman".
The probability of this event is  P(B) = 0.6.


Also, you are given that  P(A ∩ B) = 0.21.  
Here (A ∩ B) is the intersection of events A and B,  "that a student owns a credit card and is a freshman".


They ask you about the conditional probability  P( A | B).



By the definition,  the conditional probability  P( A | B)  is this ratio


    P( A | B) =  P(A ∩ B) / P(B).     (1)


Now, when you know everything, all you need to do is to substitute the given data into the formula (1)


    P( A | B) = 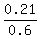 =  =  =  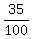= 0.35 = 35%.    ANSWER