|
Question 1149120: find the distance from(-6,6) to the line defined by y=2x+3 express as a radical or a number rounded to the nearest hundredth
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39618)   (Show Source): (Show Source):
Answer by ikleyn(52797)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
There is a remarkable formula to calculate the distance from a given point to a given straight line in a coordinate plane.
Let the straight line in a coordinate plane is defined in terms of its linear equation
a*x + b*y + c = 0,
where "a", "b" and "c" are real numbers, and let P = ( , , ) be the point in the coordinate plane.
Then the distance from the point P to the straight line is equal to
d = ) be the point in the coordinate plane.
Then the distance from the point P to the straight line is equal to
d =  .
Regarding this formula, see the lesson
The distance from a point to a straight line in a coordinate plane
in this site.
Your straight line is 2x - y + 3 = 0.
Substitute the given data a= 2, b= -1, c= 3, .
Regarding this formula, see the lesson
The distance from a point to a straight line in a coordinate plane
in this site.
Your straight line is 2x - y + 3 = 0.
Substitute the given data a= 2, b= -1, c= 3,  = -6, = -6,  = 6 into the formula to get the distance under the question = 6 into the formula to get the distance under the question
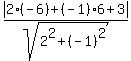 = = 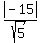 = = 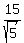 = = 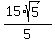 = = 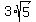 = 6.71 (approximately - rounded as requested).
Answer. The distance is = 6.71 (approximately - rounded as requested).
Answer. The distance is 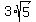 = 6.71 (approximately - rounded as requested). = 6.71 (approximately - rounded as requested).
 Straight line
Straight line  ,
the point P( ,
the point P( , , ) and the distance ) and the distance  from the point P to the straight line
from the point P to the straight line
Solved.
|
|
|
| |