Question 1149032: a fastball is hit straight up over home plate. the balls height, H( in feet), from the ground is modeled by the quadratic function defined by H(t)=16^t2+80t+5 where t is measured in seconds. at what time did the fastball reach the maximum height? solve algebraically
Answer by ikleyn(52775)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
a fastball is hit straight up over home plate. the balls height, H( in feet), from the ground is modeled
by the quadratic function defined by H(t)=16^t2+80t+5 where t is measured in seconds.
at what time did the fastball reach the maximum height? solve algebraically
~~~~~~~~~~~~~~~~~
First, the function H(t) in your post is written INCORRECTLY, having a FATAL error.
The correct form of this function is H(t) = -16t^2 + 80t + 5.
Notice the sign " - " (minus) before 16t^2 (!)
With the corrected formula, see my solution below.
The function H(t) = -16t^2 + 80t + 5 is a quadratic function, whose plot is a parabola opened down.
This quadratic function has the maximum at the value of its argument t =  , where "a" is the coefficient at t^2
and "b" is the coefficient at t.
In your case, a= -16, b= 80, so the function gets the maximum at t = , where "a" is the coefficient at t^2
and "b" is the coefficient at t.
In your case, a= -16, b= 80, so the function gets the maximum at t = 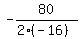 = 3.5.
So, the fastball gets the maximum height 2.5 seconds after is hit straight up. ANSWER = 3.5.
So, the fastball gets the maximum height 2.5 seconds after is hit straight up. ANSWER
Solved.
----------------
On finding the maximum/minimum of a quadratic function, see the lessons
- HOW TO complete the square to find the minimum/maximum of a quadratic function
- Briefly on finding the minimum/maximum of a quadratic function
- HOW TO complete the square to find the vertex of a parabola
- Briefly on finding the vertex of a parabola
in this site.
On solving similar problems to yours in this post, see the lessons
- Problem on a projectile moving vertically up and down
- Problem on an arrow shot vertically upward
- Problem on a ball thrown vertically up from the top of a tower
- Problem on a toy rocket launched vertically up from a tall platform
in this site.
|
|
|