SOLUTION: I'm having trouble understanding how to solve this problem. Question: Write a polynomial function with rational coefficients so that p(x)=0 has the given roots: sqrt(5), 2-i

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: I'm having trouble understanding how to solve this problem. Question: Write a polynomial function with rational coefficients so that p(x)=0 has the given roots: sqrt(5), 2-i       Log On


   

Question 1148822: I'm having trouble understanding how to solve this problem.
Question: Write a polynomial function with rational coefficients so that p(x)=0 has the given roots: sqrt(5), 2-i
Answer by ikleyn(52804) About Me  (Show Source):
You can put this solution on YOUR website!
.

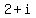Such a polynomial must have the root  -sqrt%285%29,  associated with sqrt%285%29,  and the root  2%2Bi, associated with 2-i%29%29%29.


So, the polynomial, presented as the product of linear factors is


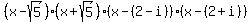    p(x) = %28x-sqrt%285%29%29%2A%28x%2Bsqrt%285%29%29%2A%28x-%282-i%29%29%2A%28x-%282%2Bi%29%29.


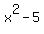The product of the first two factors is  x%5E2+-+5.


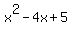The product of the last two factors is  %28x-2%29%5E2+%2B1 = x%5E2+-+4x+%2B5.


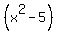So, the polynomial  p(x)  is  p(x) = %28x%5E2-5%29.%28x%5E2+-+4x+%2B+5%29.


You can multiply the last two quadratic polynomial to get the standard form, if you need.


In any case, the idea and the method are presented, so you can learn it from my post.

Solved.