Question 1148639: For #1 - #6 suppose there are two little lotteries in town, each of which sells exactly 100 tickets.
If each lottery has only one winning ticket, and you buy two tickets to the "same" lottery, what is the probability that you will have a winning ticket?
If each lottery has only one winning ticket, and you buy one ticket to each of the two lotteries, what is the probability that you will have at least one winning ticket?
If each lottery has only one winning ticket, and you buy one ticket to each of the two lotteries, what is the probability that you will have 'two' winning tickets?
If each lottery has two winning tickets, and you buy one ticket to each of the two lotteries, what is the probability that you will have at least one winning ticket?
If each lottery has two winning tickets, and you buy two tickets to the same lottery, what is the probability that you will have two winning tickets?
If each lottery has two winning tickets, and you buy two tickets to the same lottery, what is the probability that you will have at least one winning ticket?
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
I will answer ## 1), 2) and 6) only.
For #1 - #6 suppose there are two little lotteries in town, each of which sells exactly 100 tickets.
1) If each lottery has only one winning ticket, and you buy two tickets to the "same" lottery, what is the probability
that you will have  THE winning ticket?
The total number of non-ordered pairs of different tickets is THE winning ticket?
The total number of non-ordered pairs of different tickets is 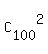 = =  . It is the sample set.
The total number of the favorable non-ordered pairs is 99. Therefore,
P = . It is the sample set.
The total number of the favorable non-ordered pairs is 99. Therefore,
P = 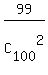 = = 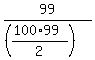 = = 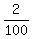 = =  ANSWER
5) If each lottery has two winning tickets, and you buy two tickets to the same lottery, what is the probability
that you will have two winning tickets?
P = ANSWER
5) If each lottery has two winning tickets, and you buy two tickets to the same lottery, what is the probability
that you will have two winning tickets?
P = 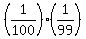 . ANSWER
6) If each lottery has two winning tickets, and you buy two tickets to the same lottery, what is the probability
that you will have at least one winning ticket?
The total number of all ordered pairs of different tickets is 100*100 = . ANSWER
6) If each lottery has two winning tickets, and you buy two tickets to the same lottery, what is the probability
that you will have at least one winning ticket?
The total number of all ordered pairs of different tickets is 100*100 = 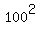 . It is the sample set.
The total number of the favorable ordered pairs is 99+99+1 = 199. Therefore,
P = . It is the sample set.
The total number of the favorable ordered pairs is 99+99+1 = 199. Therefore,
P = 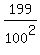 . ANSWER . ANSWER
|
|
|