Question 1148538: Given that -4 ≤ x ≤ -2 and 2 ≤ y ≤ 4, what is the largest possible value of (x+y)/x?
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52787)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
This problem is VERY SIMPLE.
Moreover, it is EXTREMELY SIMPLE, and I will show it to you right now.
Our function is 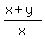 = 1 + = 1 +  . (1)
The given area is the square ABCD in quadrant QII with the vertices
A= (-4,2), B= (-2,2), C= (-2,4), D= (-4,4).
The given function, OBVIOUSLY, adds the ratio . (1)
The given area is the square ABCD in quadrant QII with the vertices
A= (-4,2), B= (-2,2), C= (-2,4), D= (-4,4).
The given function, OBVIOUSLY, adds the ratio  to the value of 1.
But this ratio to the value of 1.
But this ratio  is negative in QII.
Thus the function (1), actually, adds NEGATIVE amount to 1.
- When the function (1) will have the largest value ?
- OBVIOUSLY, when this negative addend is negative in QII.
Thus the function (1), actually, adds NEGATIVE amount to 1.
- When the function (1) will have the largest value ?
- OBVIOUSLY, when this negative addend  will have minimal absolute value.
- When this addend will have minimal absolute value.
- When this addend  will have minimal absolute value ?
- OBVIOUSLY, when positive "y" is minimal and negative "x" has maximal absolute value.
- Now, what is the point of the given square, where positive "y" is minimal and negative "x" has maximal absolute value ?
- OBVIOUSLY, this point is A= (-4,2).
Then the larges possible value of the function will have minimal absolute value ?
- OBVIOUSLY, when positive "y" is minimal and negative "x" has maximal absolute value.
- Now, what is the point of the given square, where positive "y" is minimal and negative "x" has maximal absolute value ?
- OBVIOUSLY, this point is A= (-4,2).
Then the larges possible value of the function 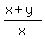 is is 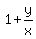 = = 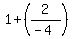 = 1 - = 1 -  = =  . ANSWER . ANSWER
Solved, explained, answered and completed.
/\/\/\/\/\/\/\/
O-o-o, tutor @greenestamps successfully retold my solution to this problem !
Congratulations (!) (!)
It seems, you invented the new way to increase the number of your posts by retelling my solutions !
Answer by greenestamps(13200)   (Show Source): (Show Source):
|
|
|