It's not (A), for that would be 
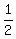
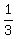
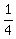
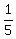 ...
... 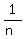 It's not (B), for that would be
It's not (B), for that would be 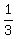
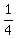
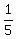
 ...
... 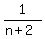 ...
It's not (C), for that would be a "two-way" sequence that goes "left and right":
...
...
It's not (C), for that would be a "two-way" sequence that goes "left and right":
...
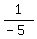
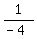
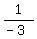
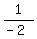

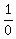




 ...
...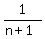 but that contains the undefined term "1/0". So that's not it.
If the following were listed I would pick this:
but that contains the undefined term "1/0". So that's not it.
If the following were listed I would pick this:
 I would hesitate to pick (D) for it says nothing about n being and integer.
But I would also hesitate to pick (E)
However, after thinking about it, I would pick (D) after all because you are
given that it is an infinite sequence, so it would not be necessary to say that
n is an integer.
Edwin
I would hesitate to pick (D) for it says nothing about n being and integer.
But I would also hesitate to pick (E)
However, after thinking about it, I would pick (D) after all because you are
given that it is an infinite sequence, so it would not be necessary to say that
n is an integer.
Edwin