Question 1148245: Find two nonnegative numbers whose sum is 9 and so that the product of one
number and the square of the other number is a maximum 10.
Found 3 solutions by greenestamps, josgarithmetic, ikleyn:
Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Not at all clear because of the poor English....
"...so that the product of ... is a maximum 10."
Are you looking for ANY two number with a sum of 9 for which the product is LESS THAN OR EQUAL TO 10? Or does the product have to be EQUAL to 10?
And by "numbers" do you mean integers? or can they be any numbers?
------------------------------------------------------
Tell your lecturer that "...is a maximum 10" is not good English if what he means is that the product is anything less than 10.
If "numbers" means integers, then there are only a small number of possibilities, and they are easy to check; there is clearly only one solution: 8 and 1.
If the numbers are integers, the problem then seems of little value, since you don't learn anything from solving it.
Since the problem apparently asks to find one solution, 8 and 1 is certainly the simplest answer (and the only answer, if the numbers are integers).
A more useful problem -- that would teach the student something about problem solving -- would be to find the complete solution set of values for x that make the product x(9-x)^2 less than or equal to 10.
Answer by josgarithmetic(39625)   (Show Source): (Show Source):
Answer by ikleyn(52848)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Find two nonnegative numbers whose sum is 9 and so that the product of one
number and the square of the other number is a maximum 10.
~~~~~~~~~~~~~~~~
Formulation of your post is NOT CORRECT and makes a few sense, if any . . .
Meanwhile, an interesting problem may stay behind it --- so I edited it, to make sense and to create really interesting problem.
My editing is as follows.
Prove that if the sum of two non-negative real number "x" and "y" is 9, x + y = 9,
then the product 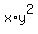 has the local maximum value of 108.
Find the values of x and y that provide this maximum. has the local maximum value of 108.
Find the values of x and y that provide this maximum.
With this reformulation, the solution is below.
Solution
If x+y = 9, then y = 9-x, and the function f(x,y) = 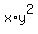 is
f(x,y) = is
f(x,y) = 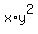 = = 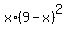 .
So, we need to find the maximum of the function of x g(x) = .
So, we need to find the maximum of the function of x g(x) = 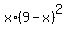 .
To find the maximum of the function g(x), take its derivative and equate it to zero.
The derivative is
g'(x) = .
To find the maximum of the function g(x), take its derivative and equate it to zero.
The derivative is
g'(x) =  - 2x*(9-x) = - 2x*(9-x) = 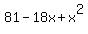 - - 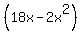 = = 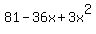 .
Equating it to zero, you get .
Equating it to zero, you get
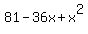 = 0, which is equivalent to = 0, which is equivalent to 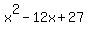 = 0.
Left side is factorable
(x-9)*(x-3) = 0.
and two solution of the quadratic equation are x= 9 and x= 3.
The value x= 9 provides the local minimum of the function f(x), while x= 3 provides the local maximum.
At x= 3, y= 9-3 = 6, and the function g(x,y) = = 0.
Left side is factorable
(x-9)*(x-3) = 0.
and two solution of the quadratic equation are x= 9 and x= 3.
The value x= 9 provides the local minimum of the function f(x), while x= 3 provides the local maximum.
At x= 3, y= 9-3 = 6, and the function g(x,y) = 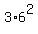 = 108. = 108.
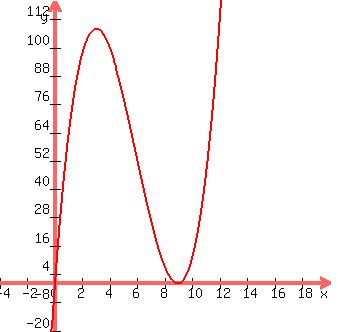 Plot g(x) = x*(9-x)^2
Plot g(x) = x*(9-x)^2
Solved.
|
|
|